高中数学不定方程和方程组试题

曲线与直线有两个相异的交点时，实数的取值范围     （     ）

A．

B．

C．

D．

已知二次函数f（x）=ax²+bx+1（a，b∈R，a＞0），设方程f（x）=x的两个实数根为x₁和x₂．
（1）如果x₁＜2＜x₂＜4，设二次函数f（x）的对称轴为x=x₀，求证：x₀＞﹣1；
（2）如果|x₁|＜2，|x₂﹣x₁|=2，求b的取值范围．

已知一次函数满足．
（1）求这个函数的解析式；
（2）若函数，求函数的零点．

定义在（0，＋∞）上的函数f（x），对于任意的m，n∈（0，＋∞），都有f（mn）＝f（m）＋f（n）成立，当x＞1时，f（x）＜0．
（1）求证：1是函数f（x）的零点；
（2）求证：f（x）是（0，＋∞）上的减函数；
（3）当f （2）＝  时，解不等式f （ax＋4）＞1．

给定两个命题: P：对任意实数都有恒成立；Q：关于的方程有实数根；如果P与Q中有且仅有一个为真命题，求实数的取值范围．

（本小题满分12分）已知是定义在上的偶函数，且当时，．
（1）求的解析式；
（2）在所给的坐标系内画出函数的草图，并求方程恰有两个不同实根时的实数的取值范围．

实系数一元二次方程有两个根，一个根在区间（0,1）内，另一个根在区间（1,2）内，则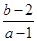的取值范围________．

已知函数在下列区间中，包含f（x）零点的区间是（ ）

A．（0,1）

B．（1,2）

C．（2,4）

D．（4，＋∞）

已知，（其中为自然对数的底数），方程有四个实数根，则实数的取值范围为             ．

若函数有两个零点，则实数的取值范围是______________．

已知函数，则函数的图象与轴有        个交点．

使得函数有零点的一个区间是（   ）

A．（0，1）

B．（1，2）

C．（2，3）

D．（3，4）

设函数，且，函数．
（1）求的解析式；
（2）若方程－b=0在 [－2，2]上有两个不同的解，求实数b的取值范围．

下列几个命题：
①函数是偶函数，但不是奇函数；
②方程的有一个正实根，一个负实根，则；
③是定义在R上的奇函数，当x＜0时，＝，则x≥ 0时，＝

④函数的值域是．
其中正确的有          ．

A．②④

B．①③④

C．①②④

D．①②③

函数的零点所在的区间是（    ）

A．

B．

C．

D．