(本小题12分)已知函数
(1)当 时,求方程
时,求方程 的解;
的解;
(2)若方程 在
在 上有实数根,求实数
上有实数根,求实数 的取值范围;
的取值范围;
(3)当 时,若对任意的
时,若对任意的 ,总存在
,总存在 ,使
,使 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)设函数 (其中
(其中 为自然对数的底数,
为自然对数的底数, ,
, ),曲线
),曲线 在点
在点 处的切线方程为
处的切线方程为 .
.
(1)求 的值;
的值;
(2)若对任意 ,函数
,函数 有且只有两个零点,求
有且只有两个零点,求 的取值范围.
的取值范围.
(本题12分)已知命题p:方程2x2+ax-a2=0在[-1,1]上有解;命题q:只有一个实数x0满足不等式x02+2ax0+2a≤0,若命题“p或q”是假命题,求a的取值范围.
定义在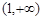 上的函数
上的函数 满足下列两个条件:
满足下列两个条件:
(1)对任意的 恒有
恒有 成立;
成立;
(2)当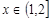 时,
时,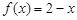 .
.
记函数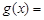
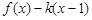 ,若函数
,若函数 恰有两个零点,则实数
恰有两个零点,则实数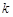 的取值范围是( )
的取值范围是( )
A.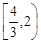 |
B.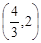 |
C.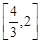 |
D. |
已知函数 ,函数
,函数 .
.
(1)当 时,函数
时,函数 的图象与函数
的图象与函数 的图象有公共点,求实数
的图象有公共点,求实数 的最大值;
的最大值;
(2)当 时,试判断函数
时,试判断函数 的图象与函数
的图象与函数 的图象的公共点的个数;
的图象的公共点的个数;
(3)函数 的图象能否恒在函数
的图象能否恒在函数 的图象的上方?若能,求出
的图象的上方?若能,求出 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.
已知命题p:函数 在(0,1)内恰有一个零点;命题q:函数
在(0,1)内恰有一个零点;命题q:函数 在
在 上是减函数,若p且
上是减函数,若p且 为真命题,则实数
为真命题,则实数 的取值范围是 ( )
的取值范围是 ( )
A. |
B.  2 2 |
C.1< ≤ 2 ≤ 2 |
D. ≤ l或 ≤ l或 >2 >2 |