已知函数 .
.
(1)当 时,求
时,求 的零点;
的零点;
(2)若方程 有三个不同的实数解,求
有三个不同的实数解,求 的值;
的值;
(3)求 在
在 上的最小值
上的最小值 .
.
已知函数 ,其中
,其中 ,若对任意的非零实数
,若对任意的非零实数 ,存在唯一的非零实数
,存在唯一的非零实数 ,使得
,使得 成立,则
成立,则 的取值范围为( )
的取值范围为( )
A. |
B. |
C. |
D. 或 或 |
已知定义在 上的单调函数
上的单调函数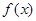 ,对
,对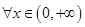 ,都有
,都有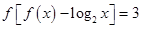 ,则方程
,则方程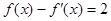 的解所在的区间是( )
的解所在的区间是( )
A.(0, ) ) |
B.(1,2) | C.( ,1) ,1) |
D.(2,3) |
设函数 (
( ),则函数
),则函数 ( )
( )
A.在区间 , , 内均有零点 内均有零点 |
B.在区间 , , 内均有零点 内均有零点 |
C.在区间 内有零点,在区间 内有零点,在区间 内无零点 内无零点 |
D.在区间 内无零点,在区间 内无零点,在区间 内有零点 内有零点 |
(本小题满分12分)已知函数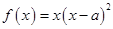 ,
,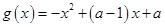 (其中
(其中 ).
).
(Ⅰ)如果函数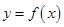 和
和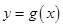 有相同的极值点,求
有相同的极值点,求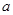 的值,并直接写出函数
的值,并直接写出函数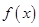 的单调区间;
的单调区间;
(Ⅱ)令 ,讨论函数
,讨论函数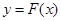 在区间
在区间 上零点的个数。
上零点的个数。
关于x的方程 (0≤x≤
(0≤x≤ )有两相异根,则实数
)有两相异根,则实数 的取值范围是__________.
的取值范围是__________.
对于函数f(x)=x|x|+px+q,现给出四个结论:
①q=0时,f(x)为奇函数;
②y=f(x)的图象关于(0,q)对称;
③p=0,q>0时,方程f(x)=0有且只有一个实数根;
④方程f(x)=0至多有两个实数根.
其中正确的结论的序号为________.
已知方程2x=10-x的根x∈(k,k+1),k∈Z,则k =________.
(本小题满分13分)已知函数 ,其中
,其中 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)证明函数 只有一个零点.
只有一个零点.