高中数学误差估计解答题

（本小题满分14分）


某校从参加高一年级期中考试的学生中随机抽取名学生，将其数学成绩（均为整数）分成六段
，…后得到如下部分频率分布直方图.观察图形的信息，回答下列问题：
(1)求分数在内的频率，并补全这个频率分布直方图；
（2）统计方法中，同一组数据常用该组区间的中点值作为代表，据此估计本次考试的平均分；
（3）用分层抽样的方法在分数段为的学生中抽取一个容量为的样本，将该样本看成一个总体，从中任取人，求至多有人在分数段的概率.

下图是总体的一样本频率分布直方图,且在［15,18)内频数为8.
(1)求样本容量;
(2)若在［12,15)内小矩形面积为0.06,求在［12,15)内频数;
(3)在（2）的条件下，求样本在［18,33)内的频率.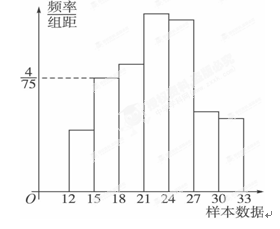

设服从试求：
（1） （2） 
（3）  （4）

某车间为了规定工时定额，需要确定加共某零件所花费的时间，为此作了四次实验，得到的数据如下：

零件的个数x(个)	2	3	4	5
加工的时间y(小时)	2.5	3	4	4.5

（1）求出y关于x的线性回归方程；
（2）试预测加工10个零件需要多少时间？

甲、乙两个野生动物保护区有相同的自然环境，且野生动物的种类和数量也大致相等．而两个保护区内每个季度发现违反保护条例的事件次数的分布列分别为：
甲保护区：

	0	1	2	3
	0.3	0.3	0.2	0.2

乙保护区：

	0	1	2
	0.1	0.5	0.4

试评定这两个保护区的管理水平．

(本小题满分12分)某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组：第1组[160，165)，第2组[165，170)，第3组[170，175)，第4组[175，180)，第5组[180，185)得到的频率分布直方图如图所示。

(Ⅰ)求第3、4、5组的频率；
(Ⅱ)为了能选拔出最优秀的学生，该校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试，求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(Ⅲ)在(Ⅱ)的前提下，学校决定在这6名学生中随机抽取2名学生接受甲考官的面试，求：第4组至少有一名学生被甲考官面试的概率?

对某400件元件进行寿命追踪调查情况频率分布如下:

寿命(h)	频 率
500～600	0.10
600～700	0.15
700～800	0.40
800～900	0.20
900～1000	0.15
合 计	1

 (1)估计元件寿命在500～800 h以内的频率；
(2)估计元件寿命在800 h以上的频率.

为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛． 为了解本次竞赛成绩情况，从中抽取了部分学生的成绩(得分均为整数，满分为100分)进行统计． 请你根据尚未完成并有局部污损的频率分布表和频数分布直方图，解答下列问题：
（1）填充频率分布表的空格(将答案直接填在表格内)；

分组	频数	频率
50．5~60．5	4	0．08
60．5~70．5		0．16
70．5~80．5	10
80．5~90．5	16	0．32
90．5~100．5
合计	50

（2）补全频数条形图；

（3）若成绩在75．5~85．5分的学生为二等奖，问获得二等奖的学生约为多少人。

（本小题满分12分）据报道，某公司的33名职工的月工资（以元为单位）如下：

职务	董事长	副董事长	董事	总经理	经理	管理员	职员
人数	1	1	2	1	5	3	20
工资	5 500	5 000	3 500	3 000	2 500	2 000	1 500

 
（1）求该公司职工月工资的平均数、中位数、众数；
（2）假设副董事长的工资从5 000元提升到20 000元，董事长的工资从5 500元提升到30 000元，那么新的平均数、中位数、众数又是什么？（精确到元）
（3）你认为哪个统计量更能反映这个公司员工的工资水平？结合此问题谈一谈你的看法．

甲、乙两位学生参加数学竞赛培训，在培训期间他们参加的次预赛成绩记录如下：甲：，，， ，  乙：，，，，
（1）用茎叶图表示这两组数据；（2）求甲、乙两人的成绩的平均数与方差;
（3）若现要从中选派一人参加数学竞赛，你认为选派哪位学生参加合适说明理由？

对400个某种型号的电子元件进行寿命追踪调查，其频率分布表如下表：

寿命（h）	频率
500600	0.10
600700	0.15
700800	0.40
800900	0.20
9001000	0.15
合计	1

（I）在下图中补齐频率分布直方图；
（II）估计元件寿命在500800h以内的概率。

某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：，，，，.

（1）求图中的值；
（2）根据频率分布直方图，估计这100名学生语文成绩的平均分；
（3）若这100名学生语文成绩某些分数段的人数（）与数学成绩相应分数段的人数（）之比如下表所示，求数学成绩在之外的人数.

分数段

 

(本小题满分12分)
某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,可见部分如下(阴影部分为损坏数据)，

据此解答如下问题:
(1) 求本次测试成绩的中位数,并求频率分布直方图中的矩形的高(用小数表示)；
(2) 若要从分数在[80，100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90，100]之间的概率.

从全校参加数学竞赛的学生的试卷中抽取一个样本，考察竞赛的成绩分布，将样本分成5组，绘成频率分布直方图，图中从左到右各小组的小长方形的高之比为1:3:6:4:2，最右边一组的频数是6，请结合直方图提供的信息，解答下列问题：

(1)样本的容量是多少？
(2)列出频率分布表；
(3)成绩落在哪个范围内的人数最多？并求出该小组的频数，频率；
(4)估计这次竞赛中，成绩高于60分的学生占总人数的百分比.

某班有48名同学，一次考试后数学成绩服从正态分布．平均分为80，标准差为10，问从理论上讲在80分至90分之间有多少人？