对某400件元件进行寿命追踪调查情况频率分布如下:
| 寿命(h) |
频 率 |
| 500~600 |
0.10 |
| 600~700 |
0.15 |
| 700~800 |
0.40 |
| 800~900 |
0.20 |
| 900~1000 |
0.15 |
| 合 计 |
1 |
(1)估计元件寿命在500~800 h以内的频率;
(2)估计元件寿命在800 h以上的频率.
相关知识点
推荐套卷
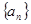 的前
的前 项和为
项和为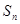 ,已知
,已知 ,
, ,求
,求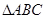 中,角
中,角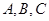 所对的边分别为
所对的边分别为 ,且
,且 是方程
是方程 的两个根,且
的两个根,且 ,求:
,求: 的度数;
的度数; 的长度。
的长度。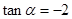 ;
;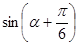 的值;
的值;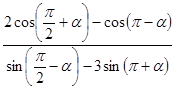 的值;
的值;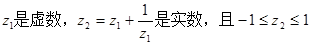
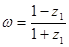 ,求证:
,求证: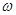 为纯虚数.
为纯虚数.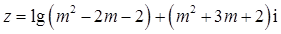 .
.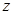 是纯虚数,求实数m的值;
是纯虚数,求实数m的值; 粤公网安备 44130202000953号
粤公网安备 44130202000953号