高中数学误差估计试题

如果数据，方差是的
平均数和方差分别是    （   ）                           

A．	B．
C．	D．

为了调查某校学生体质健康达标情况，现采用随机抽样的方法从该校抽取了m名学生进行体育测试. 根据体育测试得到了这m名学生各项平均成绩（满分100分），按照以下区间分为七组：，
，并得到频率分布直方图（如图），已知测试平均成绩在区间有20人.

（1）求m的值及中位数n；
（2）若该校学生测试平均成绩小于n，则学校应适当增加体育活动时间，根据以上抽样调查数据，该校是否需要增加体育活动时间？

某中学号召学生在今年春节期间至少参加一次社会公益活动（以下简称活动）．该校合唱团共有100名学生，他们参加活动的次数统计如图所示．

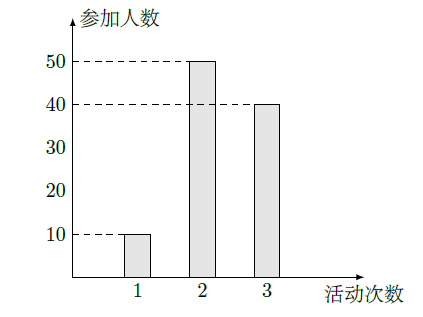
（I）求合唱团学生参加活动的人均次数；
（II）从合唱团中任意选两名学生，求他们参加活动次数恰好相等的概率．
（III）从合唱团中任选两名学生，用 $\xi$ 表示这两人参加活动次数之差的绝对值，求随机变量 $\xi$ 的分布列及数学期望 $E\xi$ ．

某城市100户居民的月平均用电量（单位：度），以[160，180），[180，200），[200，220），[220，240），[240，260），[260，280），[280，300]分组的频率分布直方图如图．

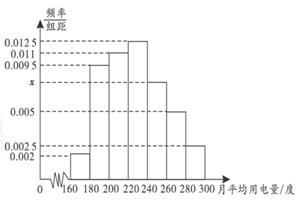
（1）求直方图中x的值；           
（2）求月平均用电量的众数和中位数；
（3）在月平均用电量为[220，240），[240，260），[260，280），[280，300]的四组用户中，用分层抽样的方法抽取11户居民，则月平均用电量在[220，240）的用户中应抽取多少户？

为了解学生身高情况，某校以 $10\%$ 的比例对全校 $700$ 名学生按性别进行分层抽样检查，测得身高情况的统计图如下：

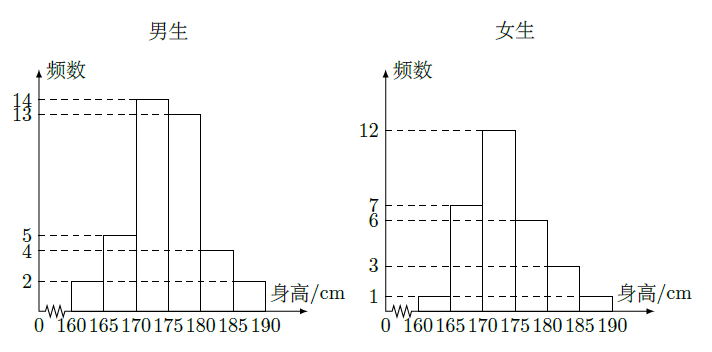
（Ⅰ）估计该校男生的人数；
（Ⅱ）估计该校学生身高在 $170~185cm$ 之间的概率；
（Ⅲ）从样本中身高在 $180~190cm$ 之间的男生中任选 $2$ 人，求至少有 $1$ 人身高在 $185~190cm$ 之间的概率.

某中学将100名高一新生分成水平相同的甲，乙两个“平行班”，每班50人。陈老师采用A,B两种不同的教学方式分别在甲，乙两个班级进行教改实验。为了解教学效果，期末考试后，陈老师对甲，乙两个班级的学生成绩进行统计分析，画出频率分布直方图（如下图），计成绩不低于90分者为“成绩优秀”.

从乙班随机抽取2名学生的成绩，记“成绩优秀”的个数为，求的分布列和数学期望.
根据频率分布直方图填写下面2x2列联表，并判断是否有的把握认为“成绩优秀”与教学方式有关.

	甲班（A方式）	乙班（B方式）	总计
成绩优秀
成绩不优秀
总计

附：

P（	0.25	0.15	0.10	0.05	0.025
k	1.323	2.072	2.706	3.841	5.024

 

某棉纺厂为了了解一批棉花的质量，从中随机抽取了100根棉花纤维的长度（棉花纤维的长度是棉花质量的重要指标），所得数据都在区间 $\left[5,40\right]$ 中，其频率分布直方图如图所示，则其抽样的100根中，有 根在棉花纤维的长度小于20 $mm$ 。

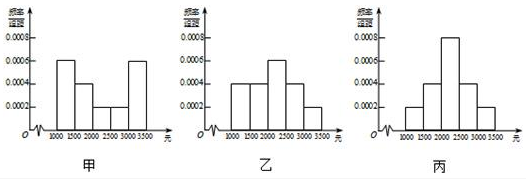
为了解本市居民的生活成本，甲、乙、丙三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查．他们将调查所得到的数据分别绘制成频率分布直方图（如图所示），记甲、乙、丙所调查数据的标准差分别为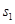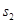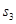，，则它们的大小关系为        ．（用“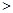”连接）

已知三个正态分布密度函数（，）的图象如下所示，则（  ）

A．，

B．，

C．，

D．，

某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组：第1组[160,165），第2组[165,170），第3组[170,175），第4组[175,180），第5组[180,185]，得到的频率分布直方图如图所示．

（1）求第3,4,5组的频率；     
（2）为了了解最优秀学生的情况，该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试，求第3,4,5组每组各抽取多少名学生进入第二轮面试．

利用随机数表法对一个容量为500编号为000，001，002，…，499的产品进行抽样检验，抽取一个容量为10的样本，若选定从第12行第4列的数开始向右读数，（下面摘取了随机数表中的第11行至第15行），根据下图，读出的第3个数是（ ）

A．584

B．114

C．311

D．160

为了了解小学五年级学生的体能情况，抽取了实验小学五年级部分学生进行踢毽子测试，将所得的数据整理后画出频率分布直方图（如图），已知图中从左到右的前三个小组的频率分别是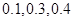，第一小组的频数是．

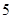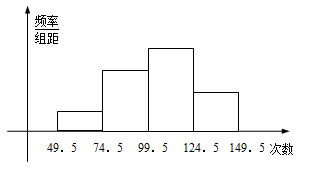
（Ⅰ）求第四小组的频率和参加这次测试的学生人数；
（Ⅱ）在这次测试中，问学生踢毽子次数的中位数落在第几小组内？
（Ⅲ）在这次跳绳测试中，规定跳绳次数在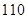以上的为优秀，试估计该校此年级跳绳成绩的优秀率是多
少？

（本小题满分12分）贵阳市某中学高三第一次摸底考试中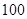名学生数学成绩的频率分布直方图如图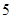所示，其中成绩分组区间是，，，，．
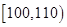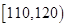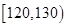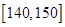（Ⅰ）求图中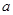的值；
（Ⅱ）根据频率分布直方图，估计这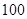名学生数学成绩的平均分；
（Ⅲ）若这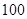名学生数学成绩某些分数段的人数（）与语文成绩相应分数段的人数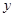（）之比如下表所示，求语文成绩在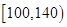之外的人数．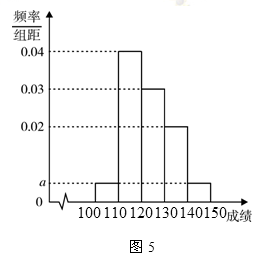

某服装商场为了了解毛衣的月销售量y（件）与月平均气温x（℃）之间的关系,随机统计了某3个月的月销售量与当月平均气温,其数据如下表：

月平均气温（°C）	11	13	12
月销售量y（件）	25	30	26

由表中数据能算出线性回归方程为               ．（参考公式：）

某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩，并用茎叶图记录分数如图所示，但部分数据不小心丢失，同时得到如下所示的频率分布表：

分数段	[50,70)	[70,90)	[90,110)	[110,130)	[130,150)	总计
频数				b
频率	a	0.25

（1）求表中a，b的值及分数在[90,100)范围内的学生人数，并估计这次考试全校学生数学成绩的及格率（分数在[90,150）内为及格）：
（2）从成绩在[100,130)范围内的学生中随机选4人，
设其中成绩在[100,110)内的人数为X，求X的分布列及数学期望.