某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185],得到的频率分布直方图如图所示.
(1)求第3,4,5组的频率;
(2)为了了解最优秀学生的情况,该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试.
相关知识点
推荐套卷
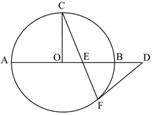
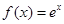 ,
,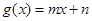 .
.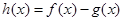 .
.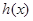 在
在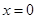 处的切线过点
处的切线过点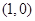 ,求
,求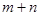 的值;
的值;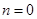 时,若函数
时,若函数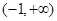 上没有零点,求
上没有零点,求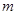 的取值范围;
的取值范围;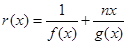 ,且
,且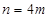 (
(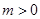 ),求证:当
),求证:当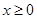 时,
时,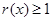 .
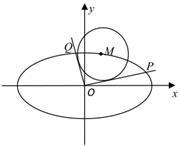
. 是椭圆
是椭圆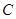 :
: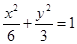 上的任一点,从原点
上的任一点,从原点 向圆
向圆 :
: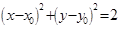 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点 、
、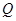 .
.
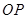 ,
,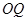 的斜率存在,并记为
的斜率存在,并记为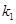 ,
,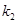 ,求证:
,求证: 为定值;
为定值;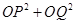 是否为定值?若是,求出该值;若不是,说明理由.
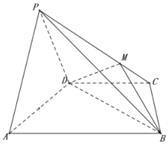
是否为定值?若是,求出该值;若不是,说明理由. 中,底面梯形
中,底面梯形 中,
中, ,平面
,平面 平面
平面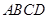 ,
,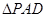 是等边三角形,已知
是等边三角形,已知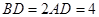 ,
, ,
, ,且
,且 .
.
 ;
; 的余弦值;
的余弦值;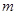 的值,使三棱锥
的值,使三棱锥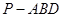 体积为三棱锥
体积为三棱锥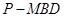 体积的3倍.
体积的3倍. 的角
的角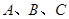 的对边分别为
的对边分别为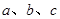 ,其面积
,其面积 ,
,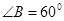 ,且
,且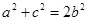 ;等差数列
;等差数列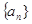 中,且
中,且 ,公差
,公差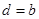 .数列
.数列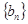 的前
的前 项和为
项和为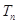 ,且
,且 ,
,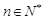 .
.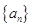 、
、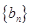 的通项公式;
的通项公式;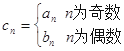 , 求数列
, 求数列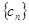 的前
的前 项和
项和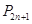 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号