福建省福州八县(市)协作校高二下学期期末联考数学(理)
5名同学去听同时进行的4个课外知识讲座,每个同学可自由选择,则不同的选择种数是( )
| A.54 | B.45 | C.5×4×3×2 | D.5×4 |
为研究变量 的线性相关性,甲、乙二人分别作了研究,利回线性回归方法
的线性相关性,甲、乙二人分别作了研究,利回线性回归方法
得到回归直线方程 ,两人计算知
,两人计算知 相同,
相同, 也相同,下列正确的是( )
也相同,下列正确的是( )
A. 重合 重合 |
B. 一定平行 一定平行 |
C. |
D.无法判断 是否相交 是否相交 |
某班有 的学生数学成绩优秀,如果从班中随机地找出5名学生,那么其中数学
的学生数学成绩优秀,如果从班中随机地找出5名学生,那么其中数学
成绩优秀的学生数 服从二项分布
服从二项分布 的值为( )
的值为( )
A. |
B. |
C. |
D. |
甲、乙两人独立地解决同一问题,甲解决这个问题的概率是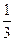 ,乙解决这个问题
,乙解决这个问题
的概率是 ,那么其中至少有一人解决这个问题的概率是( )
,那么其中至少有一人解决这个问题的概率是( )
A. |
B. |
C. |
D. |
从5位男教师和4位女教师中选出3位教师,派到3个班担任班主任(每班1位
班主任),要求这3位班主任中男、女教师都要有,则不同的选派方案共有 ( )
| A.210种 | B.420种 | C.630种 | D.840种 |
 展开式中的常数项为( )
展开式中的常数项为( )
| A.第5项 | B.第6项 | C.第5项或第6项 | D.不存在 |
把一枚骰子连续掷两次,已知在第一次抛出的是偶数点的情况下,第二次抛出的
也是偶数点的概率为 ( )
| A.1 | B. |
C. |
D. |
甲乙两队进行排球比赛,已知在一局比赛中甲队获胜的概率是 ,没有平局,
,没有平局,
若采用三局两胜制比赛,即先胜两局者获胜且比赛结束,则甲队获胜的概率等于( )
A. |
B. |
C. |
D. |
某公园现有A、B、C三只小船,A可乘3人,B船可乘2人,C船可乘1人,
今有三个成人和2个儿童分乘这些船只(每船必须坐人),为安全起见,儿童必须由大人陪
同方可乘船,他们分乘这些船只的方法有 ( )
A.48 B.36 C.30 D.18
若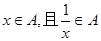 ,则称A是“伙伴关系集合”,在集合
,则称A是“伙伴关系集合”,在集合
的所有非空子集中任选一个集合,则该集合是“伙伴关系集合”的概率为 ( )
A. |
B.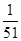 |
C. |
D. |
小王通过英语听力测试的概率是 ,他连续测试3次,那么其中恰有1次获得通过的概率是 。
,他连续测试3次,那么其中恰有1次获得通过的概率是 。
如图所示,用五种不同的颜色分别给A、B、C、D四个区域涂色,
相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同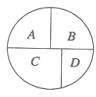 的涂色方法共有 种。
的涂色方法共有 种。
(本小题满分12分)
有20件产品,其中5件是次品,其余都是合格品,现不放回的从中依次抽2件,求:
( 1)第一次抽到次品的概率;
1)第一次抽到次品的概率;
(2)第一次和第二次都抽到次品的概率;
(3)在第一次抽到次品的条件下,第二次抽到次品的概率。
(本小题满分12分)
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(1)根据以上数据建立一个2×2列联表;
(2)判断休闲方式与性别是否有关。
(参考公式:
参考数据: )
)
(本小题满分12分)
已知m, 的展开式中,x的系数为19。
的展开式中,x的系数为19。
求 的系数的最小值,并求此时
的系数的最小值,并求此时 的系
的系 数。
数。
(本小题满分12分)
用0,1,2,3,4,5这六个数字:
(1)能组成多少个无重复数字的四位偶数?
(2)三位数中,如果十位上的数字比百位上的数字和个位上的数字都小,则这个数为凹数,
如524、746等都是凹数。那么这六个数字能组成多少个无重复数字凹数?
(本小题满分12分)
某校要用三辆汽车从新校区把教职工接到老校区,已知从新校区到老校区有两条公路,汽车走公路①堵车的概率为 ,不堵车的概率为
,不堵车的概率为 ;汽车走公路②堵车的概率为p,不堵车的概率为1—p。若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。
;汽车走公路②堵车的概率为p,不堵车的概率为1—p。若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。
(I)若三辆汽车中恰有一辆汽车被堵的概率为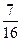 ,求走公路②堵的概率;
,求走公路②堵的概率;
(II)在(I)的条件下,求三辆汽车中恰有两辆汽车被堵的概率
(本小题满分14分)
某慈善机构举办一次募捐演出,有一万人参加,每人一张门票,每张100元,在演出过程中穿插抽奖活动,第一轮抽奖从这一万张票根中随机抽取10张,其持有者获得价值1000元的奖品,并 参加第二轮抽奖活动,第二轮抽奖由第一轮获奖者独立操作按钮,电脑随机产生两个数
参加第二轮抽奖活动,第二轮抽奖由第一轮获奖者独立操作按钮,电脑随机产生两个数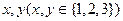 ,如果
,如果 则电脑显示“中奖”,抽奖者获得9000元奖金;否则若电脑显示“谢谢”,则不中奖。
则电脑显示“中奖”,抽奖者获得9000元奖金;否则若电脑显示“谢谢”,则不中奖。
(I)已知小曹在第一轮抽奖中被抽中,求小曹在第二轮抽奖中获奖的概率;
(II)若小叶参加了此次活动,求小叶参加此次活动收益的期望;
(III)若此次募捐除奖品和奖金外,不计其它支出,该机构想获得96万元的慈善款,问该慈善机构此 次募捐是否能达到预期目标。
次募捐是否能达到预期目标。
 ,则
,则 的值为 ( )
的值为 ( )  ,方差是
,方差是 的
的



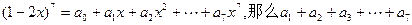 = 。
= 。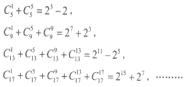
 =
=  粤公网安备 44130202000953号
粤公网安备 44130202000953号