[河南]2014届河南省豫东、豫北十所名校高中毕业班阶段测试一理数学卷

若复数z满足（2－i）z=，则z的虚部为（   ）

A．

B．

C．

D．－

已知集合A={x︱x>－2}且 ，则集合B可以是（    ）

A．{x︱x2>4 }	B．{x︱x>2}
C．{y︱}	D．（－1,0,1,2,3）

执行如图所示的程序框图，输出结果S=（    ）

下列选项中，为 的二项展开式中的一项的是（    ）

A．8

B．28

C．56

D．70

已知等比数列{a_n}的前n项和为S_n，若S=4（a₁+a₃+a₅+…+a_2n-1）,a₁a₂a₃=27,则a₆=（  ）

设△ABC的内角A、B、C所对的边分别为a，b，c，若sinB+sinC=2sinA，3a=5c，则角B=（  ）
A. 6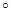0           B. 90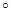            C. 12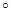0           D.150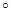

“a≥0”是“函数 在区间（－∞，0）内单调递减”的（   ）

A．充要条件	B．必要不充分条件
C．充分不必要条件	D．即不充分也不必要条件

设 ， ， 是空间任意的非零向量，且相互不共线，则以下命题中：
①（ ·）·－（· ）· =0；② ；③若存在唯一实数组 使 ，则 ， ，共面；④.
真命题的个数是（  ）

若P=，Q=，R=，则P，Q，R的大小关系是（ ）

如图，边长为a的等边三角形ABC的中线AF与中位线DE交于点G，将△ADE绕DE旋转得到△A′DE（A′ 平面ABC），则下列叙述错误的是（   ）

A. 平面A′FG⊥平面ABC
B.  BC∥平面A′DE
C. 三棱锥A′-DEF的体积最大值为
D. 直线DF与直线A′E不可能共面

在区域D：内随机取一个点，则此点到点A(1，2)的距离大于2的概率是（  ）

A．

B．

C．

D．

如图，内外两个椭圆的离心率相同，从外层椭圆顶点向内层椭圆引切线AC，BD，设内层椭圆方程为 ，若直线AC与BD的斜率之积为 ，则椭圆的离心率为（  ）

A．

B．

C．

D．

已知中心在坐标原点的双曲线C的焦距为6，离心率等于3，则双曲线C的标准方程为     .

某几何体的三视图如图所示，则该几何体的体积为       .

过点（－1,1）与曲线相切的直线有     条（以数字作答）.

在平面直角坐标系xOy中，点A（0,27 ）在y轴正半轴上，点P_n( ，0)在x轴上，记 ， ， ,则 取最大值时，的值为       .

等差数列{a_n}的前n项和为S_n，已知S₃=，且S₁，S₂，S₄成等比数列，
（1）求数列{a_n}的通项公式.
（2）若{a_n}又是等比数列，令b_n= ，求数列{b_n}的前n项和T_n.

已知函数 的图象过点（0， ），最小正周期为 ，且最小值为－1.
（1）求函数的解析式.
（2）若 ，的值域是 ，求m的取值范围.

某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩，并用茎叶图记录分数如图所示，但部分数据不小心丢失，同时得到如下所示的频率分布表：

（1）求表中a，b的值及分数在[90,100)范围内的学生人数，并估计这次考试全校学生数学成绩的及格率（分数在[90,150）内为及格）：
（2）从成绩在[100,130)范围内的学生中随机选4人，
设其中成绩在[100,110)内的人数为X，求X的分布列及数学期望.

如图，在四棱锥A-BCDE中，底面四边形BCDE是等腰梯形，BC∥DE, =45 ,O是BC的中点，AO= ,且BC=6，AD=AE=2CD=2 ，

(1)证明：AO⊥平面BCD；(2)求二面角A-CD-B的平面角的正切值.

抛物线M： 的准线过椭圆N： 的左焦点，以坐标原点为圆心，以t（t>0）为半径的圆分别与抛物线M在第一象限的部分以及y轴的正半轴相交于点A与点B，直线AB与x轴相交于点C.

（1）求抛物线M的方程.
（2）设点A的横坐标为x₁，点C的横坐标为x₂，曲线M上点D的横坐标为x₁+2，求直线CD的斜率.

已知函数 .
（1）若 的极小值为1，求a的值.
（2）若对任意 ，都有 成立，求a的取值范围.