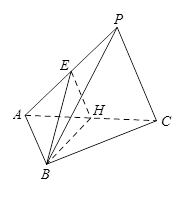
如图,在三棱锥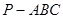 中,△
中,△ 是边长为
是边长为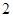 的正三角形,
的正三角形,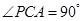 ,
, 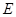 ,
,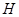 分别为
分别为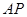 ,
,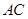 的中点,
的中点,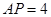 ,
,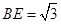 .
. 
(Ⅰ)求证: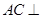 平面
平面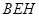 ;
;
(Ⅱ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
在四棱柱 中,
中, 平面
平面 ,底面
,底面 是边长为
是边长为 的正方形,侧棱
的正方形,侧棱 的长为
的长为 ,
, 为侧棱
为侧棱 上的动点(包括端点),则
上的动点(包括端点),则
A.对任意的 , , ,存在点 ,存在点 ,使得 ,使得 |
B.当且仅当 时,存在点 时,存在点 ,使得 ,使得 |
C.当且仅当 时,存在点 时,存在点 ,使得 ,使得 |
D.当且仅当 时,存在点 时,存在点 ,使得 ,使得 |
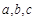 表示直线,
表示直线,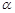 表示平面,下列命题正确的是( )
表示平面,下列命题正确的是( )
A.若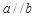 , ,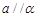 ,则 ,则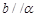 |
B.若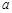 ⊥ ⊥ , ,  ⊥ ⊥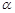 ,则 ,则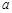 ⊥ ⊥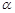 |
C.若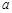 ⊥ ⊥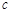 , , ⊥ ⊥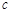 ,则 ,则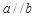 |
D.若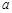 ⊥ ⊥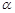 , , ⊥ ⊥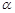 ,则 ,则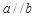 |
(本小题满分14分)如图,在四棱锥P-ABCD中,底面ABCD是正方形,
侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
⑴求证:PA∥平面BDE;
⑵求证:平面BDE⊥平面PBC.
(本小题满分12分)
如图,已知 ,
, 分别是正方形
分别是正方形 边
边 ,
, 的中点,
的中点, 与
与 交于点
交于点 ,
, 都垂直于平面
都垂直于平面 ,且
,且 ,
, 是
是 中点.
中点.
(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
如图,在三棱锥
中,
在底面
的射影为
的中点,
为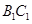
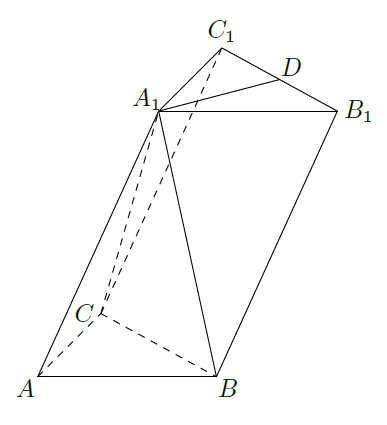
(1)证明:
;
(2)求直线
和平面
所成的角的正弦值.
(本小题共12分)如图,四棱锥P - ABCD的底面是边长为1的正方形,PA⊥底面ABCD,E、F分别为AB、PC的中点.
(1)若PA = 1,求证:EF⊥平面PCD;
(2)若PA = 2,试问在线段EF上是否存在点Q,使得二面角 Q - AP - D的余弦值为 ?若存在,确定点Q的位置;若不存在,请说明理由.
?若存在,确定点Q的位置;若不存在,请说明理由.
若m,n是两条不同的直线,a,b是两个不同的平面,则下列命题中正确的是 ( )
| A.a∥b, mÌa, nÌbÞ m∥n | B.a⊥b, n∥a, m⊥bÞn⊥m |
| C.m∥n, m∥aÞ n∥a | D.m∥n, m⊥aÞn⊥a |
如图,PA⊥平面ABCD,矩形ABCD的边长AB=1,BC=2,E为BC的中点.
(1)证明:PE⊥DE;
(2)如果PA=2,求异面直线AE与PD所成的角的大小.
观察下面的演绎推理过程,判断正确的是( )
大前提:若直线a⊥直线l,且直线b⊥直线l,则a∥b.
小前提:正方体ABCD-A1B1C1D1中,A1B1⊥AA1,且AD⊥AA1.
结论:A1B1∥AD.
A.推理正确
B.大前提出错导致推理错误
C.小前提出错导致推理错误
D.仅结论错误