上海市普陀区高三二模文科数学试卷
一个袋子中有7个除颜色外完全相同的小球,其中5个红色,2个黑色.经过充分混合后,从袋中随机地取出2个小球.则至少有一个黑球的概率为 (结果用最简分数作答).
来源:2015届上海市普陀区高三二模文科数学试卷
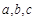 表示直线,
表示直线,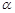 表示平面,下列命题正确的是( )
表示平面,下列命题正确的是( )
A.若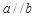 , ,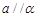 ,则 ,则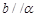 |
B.若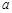 ⊥ ⊥ , ,  ⊥ ⊥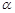 ,则 ,则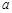 ⊥ ⊥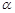 |
C.若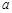 ⊥ ⊥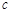 , , ⊥ ⊥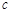 ,则 ,则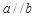 |
D.若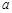 ⊥ ⊥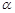 , , ⊥ ⊥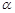 ,则 ,则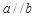 |
来源:2015届上海市普陀区高三二模文科数学试卷
”直线与抛物线相切”是“直线与抛物线只有一个公共点”的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.非充分非必要条件 |
来源:2015届上海市普陀区高三二模文科数学试卷
在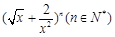 的展开式中,若第五项的系数与第三项的系数之比为56:3,则展开式中的常数项是( )
的展开式中,若第五项的系数与第三项的系数之比为56:3,则展开式中的常数项是( )
| A.第2项 | B.第3项 | C.第4项 | D.第5项 |
来源:2015届上海市普陀区高三二模文科数学试卷
已知 均为正整数,记
均为正整数,记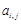 为矩阵
为矩阵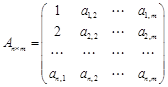 中第
中第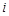 行、第
行、第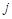 列的元素,且
列的元素,且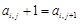 ,
,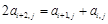 (其中
(其中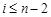 ,
,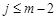 );给出结论:①
);给出结论:①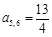 ;②
;②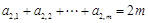 ;③
;③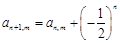 ④若
④若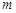 为常数,则
为常数,则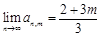 .其中正确的个数是( )
.其中正确的个数是( )
| A.0个 | B.1个 | C.2个 | D.3个 |
来源:2015届上海市普陀区高三二模文科数学试卷
本题满分12分,第1小题6分,第2小题6分)
在正方体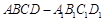 中,
中,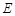 是棱
是棱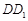 的中点,四棱锥
的中点,四棱锥 的体积为
的体积为 ,求异面直线
,求异面直线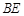 与
与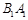 所成的角的大小(结果用反三角函数值表示).
所成的角的大小(结果用反三角函数值表示).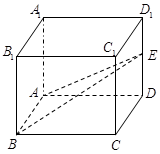
来源:2015届上海市普陀区高三二模文科数学试卷
(本题满分14分,第1小题6分,第2小题8分)
已知函数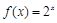 的反函数为
的反函数为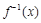
(1)若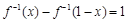 ,求实数
,求实数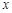 的值;
的值;
(2)若关于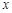 的方程
的方程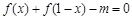 在区间
在区间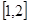 内有解,求实数
内有解,求实数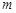 的取值范围;
的取值范围;
来源:2015届上海市普陀区高三二模文科数学试卷
(本题满分16分,第1小题4分,第2小题7分,第3小题5分)
如图,射线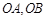 所在的直线的方向向量分别为
所在的直线的方向向量分别为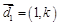 ,
, ,点
,点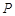 在
在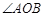 内,
内, 于
于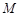 ,
,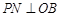 于
于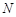 ;
;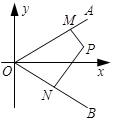
(1)若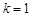 ,
,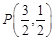 ,求
,求 的值;
的值;
(2)若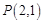 ,
,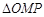 的面积为
的面积为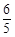 ,求
,求 的值;
的值;
(3)已知 为常数,
为常数,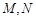 的中点为
的中点为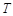 ,且
,且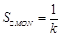 ,当
,当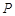 变化时,求动点
变化时,求动点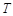 轨迹方程;
轨迹方程;
来源:2015届上海市普陀区高三二模文科数学试卷
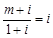 (
(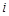 为虚数单位),则实数
为虚数单位),则实数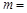 .
.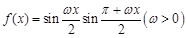 的最小正周期为
的最小正周期为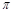 ,则
,则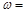 .
.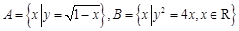 ,则
,则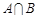 .
.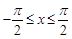 ,则函数
,则函数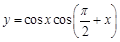 的单调递减区间为 .
的单调递减区间为 .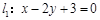 与
与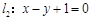 的夹角的大小为 .(结果用反三角函数表示)
的夹角的大小为 .(结果用反三角函数表示)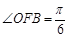 ,
, ,则以
,则以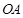 为长半轴,
为长半轴,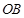 为短半轴,
为短半轴,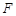 为左焦点的椭圆的标准方程为 .
为左焦点的椭圆的标准方程为 .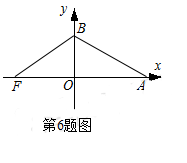
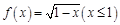 ,若函数
,若函数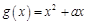 是偶函数,则
是偶函数,则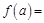 .
.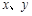 满足
满足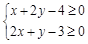 ,则
,则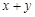 的最小值为 .
的最小值为 .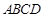 的边长为1,且
的边长为1,且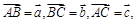 则
则 .
.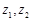 满足
满足 ,
,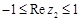 ,
, ,若
,若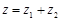 ,则
,则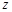 在复平面上对应的点组成的图形的面积为 .
在复平面上对应的点组成的图形的面积为 .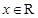 ,用记号
,用记号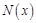 表示不小于实数的最小整数,例如
表示不小于实数的最小整数,例如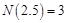 ,
,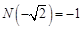 ,
,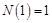 ;则函数
;则函数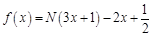 的所有零点之和为 .
的所有零点之和为 .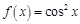 ,
, .
.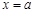 是函数
是函数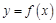 的图像的一条对称轴,求
的图像的一条对称轴,求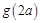 的值;
的值;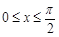 ,求
,求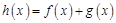 的值域.
的值域.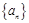 的前
的前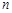 项和为
项和为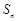 ,且
,且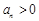 ,
,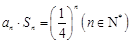
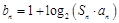 ,求数列
,求数列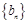 的前
的前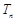 ;
;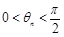 ,
,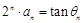 ,求证:数列
,求证:数列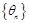 为等比数列,并求出其通项公式;
为等比数列,并求出其通项公式;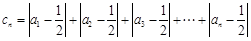 ,若对任意的
,若对任意的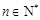 ,
,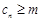 恒成立,求实数
恒成立,求实数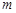 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号