高中数学立体图形的结构特征试题

已知一个高度不限的直三棱柱，，，，点是侧棱上一点，过作平面截三棱柱得截面，给出下列结论：①是直角三角形；②是等边三角形；③四面体为在一个顶点处的三条棱两两垂直的四面体，其中有可能成立的结论的个数是（）

A．0

B．1

C．2

D．3

已知圆锥的底面半径为，高为，在它的所有内接圆柱中，全面积的最大值为( )

A．

B．

C．

D．

如图,正方体的棱长为1,P为BC的中点,Q为线段上的动点,过点A,P,Q的平面截该正方体所得的截面记为S．则下列命题正确的是_____（写出所有正确命题的编号）．

①当时,S为四边形;
②当时,S为等腰梯形;
③当时,S与的交点R满足;
④当时,S为六边形;
⑤当时,S的面积为．

如图所示，在正三角形ABC中，D，E，F分别为各边的中点，G，H分别为DE，AF的中点，将△ABC沿DE，EF，DF折成正四面体P－DEF，则四面体中异面直线PG与DH所成角的余弦值为________．

长方体的三个相邻面的面积分别是，这个长方体的顶点都在同一个球面上，则这个球的表面积为（）

A．

B．

C．

D．

如图所示，在正三角形ABC中，D，E，F分别为各边的中点，G，H分别为DE，AF的中点，将△ABC沿DE，EF，DF折成正四面体P－DEF，则四面体中异面直线PG与DH所成的角的余弦值为________．

如图所示，ABCD－A₁B₁C₁D₁是棱长为a的正方体，M，N分别是下底面的棱A₁B₁，B₁C₁的中点，P是上底面的棱AD上的一点，AP＝，过P，M，N的平面交上底面于PQ，Q在CD上，则PQ＝__________．

如图，PA⊥⊙O所在的平面，AB是⊙O的直径，C是⊙O上的一点，E，F分别是点A在PB，PC上的射影，给出下列结论：

①AF⊥PB；②EF⊥PB；③AF⊥BC；④AE⊥平面PBC.其中正确命题的序号是________．

底面为正三角形且侧棱与底面垂直的三棱柱称为正三棱柱，则半径为的球的内接正三棱柱的体积的最大值为__________.

已知四棱锥的底面是边长为 $\sqrt{2}$的正方形，侧棱长均为 $\sqrt{5}$．若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点，另一个底面的圆心为四棱锥底面的中心，则该圆柱的体积为_____________．

一个正方体的内切球、外接球、与各棱都相切的球的半径之比为（）

A．

B．

C．

D．

设E、F、G分别为四面体ABCD的棱BC、CD、DA的中点，则此四面体中与过E、F、G的截面平行的棱有 条．

在半径为1的球面上有不共面的四个点A，B，C，D且，，，则等于（）

A．2

B．4

C．8

D．16

在半径为5的球面上有不同的四点A、B、C、D，若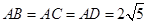，则平面BCD被球所截面图形的面积为.

等边三角形ABC的边长为2，将它沿高AD翻折，使点B与点C问的距离为，此时四面体
ABCD外接球体积为．