高中数学立体图形的结构特征试题

已知棱长为2的正方体，是过顶点圆上的一点，为中点，则与面所成角余弦值的取值范围是（）

A．

B．

C．

D．

如图，在三棱锥中，，，平面平面，为中点，点分别为线段上的动点（不含端点），且，则三棱锥体积的最大值为________．

如图，圆锥的轴截面SAB是边长为2的等边三角形，O为底面中心，M为SO中点，动点P在圆锥底面内（包括圆周），若AM⊥MP，则点P形成的轨迹长度为

已知一个三棱柱，其底面是正三角形，且侧棱与底面垂直，一个体积为的球体与棱柱的所有面均相切，那么这个三棱柱的表面积是( )

A．

B．

C．

D．

平面内有个圆中，每两个圆都相交，每三个圆都不交于一点，若该个圆把平面分成个区域，那么 ．

设A、B、C、D是半径为2的球面上的四点，且满足，的最大值是_______ ．

已知直三棱柱ABC-A₁B₁C₁的各棱长均为1,棱BB₁所在直线上的动点M满足,AM与侧面BB₁C₁C所成的角为,若,则的取值范围是（）

A．

B．

C．

D．

已知三棱锥中，，，，，，则关于该三棱锥的下列叙述正确的为（）

A．表面积	B．表面积为
C．体积为	D．体积为

在直三棱柱中，底面为直角三角，，，是上一动点，则的最小值是________．

已知四棱锥的底面是边长为 $\sqrt{2}$的正方形，侧棱长均为 $\sqrt{5}$．若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点，另一个底面的圆心为四棱锥底面的中心，则该圆柱的体积为_____________．

一个正方体的内切球、外接球、与各棱都相切的球的半径之比为（）

A．

B．

C．

D．

设E、F、G分别为四面体ABCD的棱BC、CD、DA的中点，则此四面体中与过E、F、G的截面平行的棱有 条．

在半径为1的球面上有不共面的四个点A，B，C，D且，，，则等于（）

A．2

B．4

C．8

D．16

在半径为5的球面上有不同的四点A、B、C、D，若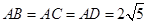，则平面BCD被球所截面图形的面积为.

等边三角形ABC的边长为2，将它沿高AD翻折，使点B与点C问的距离为，此时四面体
ABCD外接球体积为．