我国科研人员屠呦呦法相从青篙中提取物青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间r(小时)之间近似满足如图所示的曲线
(1)写出第一服药后y与t之间的函数关系式y=f(x);
(2)据进一步测定:每毫升血液中含药量不少于 微克时,治疗有效,求服药一次后治疗有效的时间是多长?
微克时,治疗有效,求服药一次后治疗有效的时间是多长?
为治疗一种慢性病,某医药研究所研究出一种新型药物,病人按规定的剂量服用该药物后,测得每毫升血液中含药量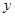 (毫克)与时间
(毫克)与时间 (小时)满足:前1小时内成正比例递增,1小时后按指数型函数
(小时)满足:前1小时内成正比例递增,1小时后按指数型函数 (
( 为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.
为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.
(1)求函数 的解析式;
的解析式;
(2)已知每毫升血液中含药量不低于0.5毫克时有治疗效果,低于0.5毫克时无治疗效果.求病人一次服药后的有效治疗时间为多少小时?
为了预防甲型H1N1流感,某学校对教室用药薰消毒法进行消毒,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与t时间(小时)成正比,药物释放完毕后,y与t之间的函数关系式为 (a为常数)如下图所示,根据图中提供的信息,回答下列问题.
(a为常数)如下图所示,根据图中提供的信息,回答下列问题.
(1)从药物释放开始,求每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那么从药物释放开始至少需要经过多少小时后,学生才可能回到教室.
A市积极倡导学生参与绿色环保活动,其中代号为“环保卫士——12369”的绿色环保活动小组对2014年1月——2014年12月(一年)内空气质量指数 进行监测,下表是在这一年随机抽取的100天的统计结果:
进行监测,下表是在这一年随机抽取的100天的统计结果:
| 指数API |
[0,50] |
(50,100] |
(100,150] |
(150,200] |
(200,250] |
(250,300] |
>300 |
| 空气质量 |
优 |
良 |
轻微污染 |
轻度污染 |
中度污染 |
中重度污染 |
重度污染 |
| 天数 |
4 |
13 |
18 |
30 |
9 |
11 |
15 |
(1)若A市某企业每天由空气污染造成的经济损失P(单位:元)与空气质量指数 (记为t)的关系
(记为t)的关系
为: ,在这一年内随机抽取一天,估计该天经济损失
,在这一年内随机抽取一天,估计该天经济损失 元的概率;
元的概率;
(2)若本次抽取的样本数据有30天是在供暖季节,其中有8天为重度污染,完成 列联表,并判断是
列联表,并判断是
否有 的把握认为A市本年度空气重度污染与供暖有关?
的把握认为A市本年度空气重度污染与供暖有关?
| |
非重度污染 |
重度污染 |
合计 |
| 供暖季 |
|
|
|
| 非供暖季节 |
|
|
|
| 合计 |
|
|
100 |
下面临界值表供参考.
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
参考公式: ,其中
,其中 .
.
某公司的广告费支出x与销售额y(单位:万元)之间有下列对应数据
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
50 |
70 |
(1)画出散点图,并判断广告费与销售额是否具有相关关系;
(2)根据表中提供的数据,用最小二乘法求出y与x的回归方程 ;
;
(3)预测销售额为115万元时,大约需要多少万元广告费。
参考公式:回归方程为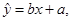 其中
其中 ,
, 
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗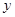 (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
 |
3 |
4 |
5 |
6 |
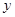 |
2.5 |
3 |
4 |
4.5 |
( )
)
(1)请根据上表提供的数据,用最小二乘法求出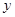 关于
关于 的线性回归方程
的线性回归方程 ;
;
(2)已知该厂技术改造前100吨甲产品能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(本小题满分12分)
某研究机构对高三学生的记忆力 和判断力
和判断力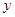 进行统计分析,得下表数据:
进行统计分析,得下表数据:
| x |
6 |
8 |
10 |
12 |
| y |
2 |
3 |
5 |
6 |
(1)画出散点图并指出 与
与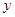 之间是正相关还是负相关 ;
之间是正相关还是负相关 ;
(2)请根据上表提供的数据,用最小二乘法求出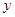 关于
关于 的线性回归方程
的线性回归方程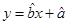 ;
;
其中(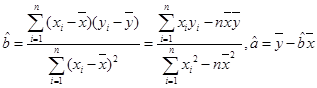 )
)
(3)记忆力为14的同学的判断力约为多少?
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,求出 关于
关于 的线性回归方程
的线性回归方程 ;
;
(3)已知该厂技术改造前 吨甲产品能耗为
吨甲产品能耗为 吨标准煤;试根据(2)求出的线性回归方程,预测生产
吨标准煤;试根据(2)求出的线性回归方程,预测生产 吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
某地最近十年粮食需求量逐年上升,下表是部分统计数据:
| 年份 |
2002 |
2004 |
2006 |
2008 |
2010 |
| 需求量(万吨) |
236 |
246 |
257 |
276 |
286 |
(Ⅰ)利用所给数据求年需求量与年份之间的回归直线方程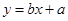 ;
;
(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该地2012年的粮食需求量.
一次考试中,五名学生的数学、物理成绩如下表所示:
| 学生 |
A1 |
A2 |
A3 |
A4 |
A5 |
| 数学(x分) |
89 |
91 |
93 |
95 |
97 |
| 物理(y分) |
87 |
89 |
89 |
92 |
93 |
(1)请在所给的直角坐标系中画出它们的散点图
(2)并求这些数据的线性回归方程 =bx+a.
=bx+a.
附:线性回归方程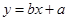 中,
中,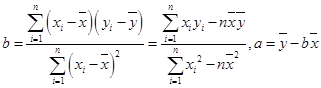
其中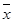 ,
, 为样本平均值,线性回归方程也可写为
为样本平均值,线性回归方程也可写为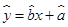 .
.
某地区2008年至2014年农村居民家庭纯收入y(单位:千元)的数据如下表:
| 年份 |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
2014 |
年份代号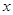 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 人均纯收入y |
2.9 |
3.3 |
3.6 |
4.4 |
4.8 |
5.2 |
5.9 |
(Ⅰ)求y关于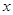 的线性回归方程;
的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2008年至2014年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2016年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: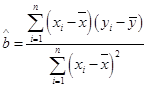 ,
, .
.
(本小题满分12分)
从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得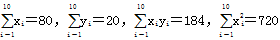 .
.
(1)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程y=bx+a中,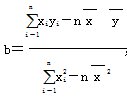 ,a=
,a= -b
-b 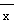 ,其中
,其中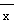 ,
, 为样本平均值.
为样本平均值.
经过长期的观测得到:在交通繁忙的时段内,蚌埠市解放路某路段汽车的车流量 (千辆/h)与汽车的平均速度
(千辆/h)与汽车的平均速度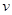 (
(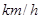 )之间的函数关系为
)之间的函数关系为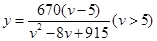 。
。
(1)在该时段内,当汽车的平均速度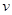 为多少时车流量最大,最大车流量为多少?(精确到0.1千辆/h)
为多少时车流量最大,最大车流量为多少?(精确到0.1千辆/h)
(2)若要求在该时段内车流量超过10千辆/h,则汽车的平均速度应在什么范围内?
(本小题满分18分)某位同学进行寒假社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了1月11日至1月15日的白天平均气温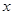 (°C)与该奶茶店的这种饮料销量
(°C)与该奶茶店的这种饮料销量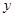 (杯),得到如下数据:
(杯),得到如下数据:
| 日 期 |
1月11日 |
1月12日 |
1月13日 |
1月14日 |
1月15日 |
平均气温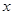 (°C) (°C) |
9 |
10 |
12 |
11 |
8 |
销量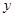 (杯) (杯) |
23[] |
25 |
30 |
26 |
21 |
(1)若从这五组数据中随机抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出y关于x的线性回归方程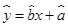 .
.
(参考公式: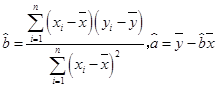 .)
.)