下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
 |
3 |
4 |
5 |
6 |
 |
2.5 |
3 |
4 |
4.5 |
( )
)
(1)请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程
的线性回归方程 ;
;
(2)已知该厂技术改造前100吨甲产品能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
相关知识点
推荐套卷
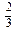 ,服用B有效的概率为
,服用B有效的概率为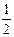 。
。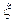 表示这3个试验组中甲类组的个数,求
表示这3个试验组中甲类组的个数,求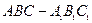 中,AC="BC," AC⊥BC,点D是A1B1中点.
中,AC="BC," AC⊥BC,点D是A1B1中点.  ,求二面角D- AC1-A1的余弦值.
,求二面角D- AC1-A1的余弦值.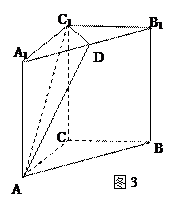
 、
、 、
、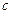 分别是△ABC的三个内角A、B、C的对边,设
分别是△ABC的三个内角A、B、C的对边,设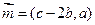 ,
,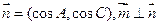 .
. ,求
,求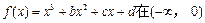 上是增函数,在[0,2]上是减函数,且方程
上是增函数,在[0,2]上是减函数,且方程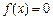 有三个根,它们分别为
有三个根,它们分别为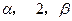 .
.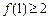 ;
;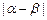 的取值范围.
的取值范围.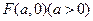 ,动点
,动点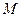 、
、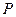 分别在
分别在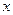 、
、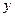 轴上运动,满足
轴上运动,满足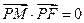 ,
,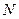 为动点,并且满足
为动点,并且满足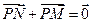 .
.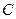 的方程;
的方程;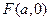 的直线
的直线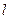 (不与
(不与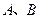 两点,设点
两点,设点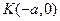 ,
,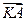 与
与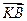 的夹角为
的夹角为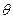 ,求证:
,求证: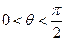 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号