某公司的广告费支出x与销售额y(单位:万元)之间有下列对应数据
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
50 |
70 |
(1)画出散点图,并判断广告费与销售额是否具有相关关系;
(2)根据表中提供的数据,用最小二乘法求出y与x的回归方程 ;
;
(3)预测销售额为115万元时,大约需要多少万元广告费。
参考公式:回归方程为 其中
其中 ,
, 
相关知识点
推荐套卷

 ;(Ⅱ)若
;(Ⅱ)若 ,求
,求 的取值范围.
的取值范围.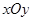 中,以坐标原点为极点,
中,以坐标原点为极点,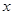 轴正半轴为极轴建立极坐标系,半圆
轴正半轴为极轴建立极坐标系,半圆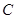 的极坐标方程为
的极坐标方程为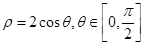
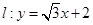 垂直,根据(Ⅰ)中你得到的参数方程,确定D的坐标.
垂直,根据(Ⅰ)中你得到的参数方程,确定D的坐标.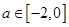 ,已知函数
,已知函数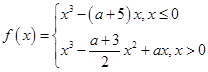 ,
,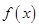 在区间
在区间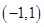 内单调递减,在区间
内单调递减,在区间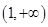 内单调递增;
内单调递增;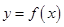 在点
在点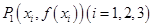 处的切线相互平行,且
处的切线相互平行,且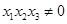 ,
,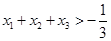
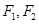 分别是椭圆
分别是椭圆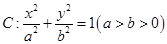 的左右焦点,
的左右焦点,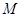 是
是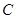 上一点且
上一点且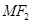 与
与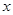 轴垂直,直线
轴垂直,直线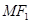 与
与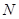 .
.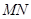 的斜率为
的斜率为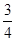 ,求
,求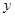 轴上的截距为2,且
轴上的截距为2,且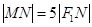 ,求
,求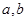
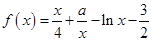 ,其中
,其中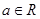 ,且曲线
,且曲线 在点
在点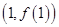 处的切线垂直于直线
处的切线垂直于直线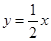
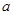 的值;
的值; 的单调区间及极值.
的单调区间及极值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号