（满分12分）假设关于某设备的使用年限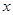
和所支出的维修费用
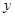（万元）有如下的统计资料：
| 使用年限 |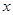
 |
 |
 |
 |
 |
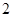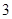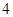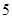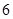| 维修费用 |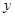
 |
 |
 |
 |
 |
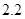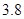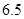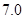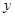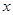若由资料知对呈线性相关关系。
（1）请画出上表数据的散点图；
（2）请根据最小二乘法求出线性回归方程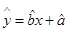
的回归系数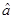
,
．
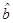（3）估计使用年限为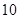
年时，维修费用是多少？
，
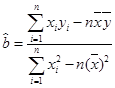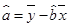
（满分12分）假设关于某设备的使用年限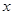
和所支出的维修费用
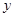（万元）有如下的统计资料：
| 使用年限 |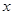
 |
 |
 |
 |
 |
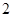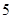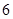| 维修费用 |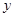
 |
 |
 |
 |
 |
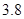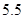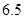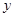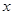若由资料知对呈线性相关关系。
（1）请画出上表数据的散点图；
（2）请根据最小二乘法求出线性回归方程
的回归系数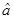
,
．
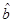（3）估计使用年限为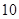
年时，维修费用是多少？
，
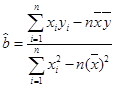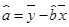
某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作四次试验，得到的数据如下：
| 零件的个数x（个） |
2 |
3 |
4 |
5 |
| 加工的时间y（小时） |
2．5 |
3 |
4 |
4．5 |
（1）已知零件个数与加工时间线性相关，求出y关于x的线性回归方程；
（2）试预测加工10个零件需要多少时间？
下表数据是水温度x（℃）对黄酮延长性y（%）效应的试验结果，y是以延长度计算的，且对于给定的x，y为变量．
| x（℃） |
300 |
400 |
500 |
600 |
700 |
800 |
| y（%） |
40 |
50 |
55 |
60 |
67 |
70 |
（1）求y关于x的回归方程；
（2）估计水温度是1 000 ℃时，黄酮延长性的情况．
（可能用到的公式：
，
，其中
、
是对回归直线方程
中系数
、
按最小二乘法求得的估计值）
某市电力公司在电力供不应求时期，为了居民节约用电，采用“阶梯电价”方法计算电价，每月用电不超过
度时，按每度
元计费，每月用电超过度时，超过部分按每度
元计费，每月用电超过
度时，超过部分按每度
元计费.
（1）设每月用电
度，应交电费
元，写出关于的函数；
（2）已知小王家第一季度缴费情况如下：
| 月份 |
1 |
2 |
3 |
合计 |
| 缴费金额 |
87元 |
62元 |
45元8角 |
194元8角 |
问：小王家第一季度共用了多少度电？
生产
，
两种元件，其质量按测试指标划分为：指标大于或等于82为正品，小于82为次品，现随机抽取这两种元件各100件进行检测，检测结果统计如下：
| 测试指标 |
 |
 |
 |
 |
 |
| 元件 |
8 |
12 |
40 |
32 |
8 |
| 元件 |
7 |
18 |
40 |
29 |
6 |
（Ⅰ）试分别估计元件、元件为正品的概率；
（Ⅱ）生产一件元件，若是正品可盈利50元，若是次品则亏损10元；生产一件元件，若是正品可盈利100元，若是次品则亏损20元，在（Ⅰ）的前提下
（i）求生产5件元件所获得的利润不少于300元的概率；
（ii）记
为生产1件元件和1件元件所得的总利润，求随机变量的分布列和期望．
某种产品的广告费支出x与销售额y（单位：百万元）之间有如下对应数据：
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
50 |
70 |
（1）画出散点图；
（2）求回归直线方程；
（3）试预测广告费支出为10百万元时，销售额多大？
某种产品的广告费支出x与销售额y（单位：百万元）之间有如下对应数据：
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
50 |
70 |
（1）画出散点图；
（2）求回归直线方程；
（3）试预测广告费支出为10百万元时，销售额多大？
（可能用到的公式：
，
，其中
、
是对回归直线方程
中系数
、
按最小二乘法求得的估计值）
假设关于某设备的使用年限
和所支出的维修费用
（万元），有如下的统计资料：
| 使用年限 |
2 |
3 |
4 |
5 |
6 |
| 维修费用 |
2．2 |
3．8 |
5．5 |
6．5 |
7．0 |
若由资料知道对呈线性相关关系．
附：
试求：
（1）线性回归方程
的回归系数．
（2）估计使用年限为10年时，维修费用是多少？
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下
| |
男 |
女 |
合计 |
| 需要 |
40 |
30 |
|
| 不需要 |
160 |
270 |
|
| 合计 |
|
|
|
（1）将表格填写完整，并估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
（2）能否在犯错误的概率不超过0.01的前提下认为该地区的老年人是否需要志愿者提供帮助与性别有关系?
（3）根据（2）的结论,能否提出更好的调查方法估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由。
附表：
| P(K2≥k) |
0.050 |
0.010 |
0.001 |
| k |
3.841 |
6.635 |
10.828 |
我市某高中的一个综合实践研究小组欲研究昼夜温差大小与患感冒人数多少之间的关系，他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数，得到如下资料：
| 日 期 |
1月10日 |
2月10日 |
3月10日 |
4月10日 |
5月10日 |
6月10日 |
昼夜温差 (°C) |
10 |
11 |
13 |
12 |
8 |
6 |
就诊人数 (个) |
22 |
25 |
29 |
26 |
16 |
12 |
该综合实践研究小组确定的研究方案是：先从这六组数据中选取2组，用剩下的4组数据求线性回归方程，再用被选取的2组数据进行检验.
（1）若选取的是1月与6月的两组数据，请根据2至5月份的数据，求出关于的线性回归方程
．
（2）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人，则认为得到的线性回归方程是理想的，试问该小组所得线性回归方程是否理想?
参考数据： 
；
.
以下是某地搜集到的新房屋的销售价格
（万元）和房屋的面积
（
）的数据 ，若由资料可知对呈线性相关关系。
|
80 |
90 |
100 |
110 |
120 |
| y |
48 |
52 |
63 |
72 |
80 |
试求:（1）线性回归方程；
（2）根据（1）的结果估计当房屋面积为
时的销售价格.
参考公式：
某种产品的广告费支出
与销售额
（单位：百万元）之间有如下对应数据：
|
2 |
4 |
5 |
6 |
8 |
|
30 |
40 |
60 |
50 |
70 |
（1）求回归直线方程。
（2）试预测广告费支出为10百万元时，销售额多大？
某人摆一个摊位卖小商品，一周内出摊天数x与盈利y(百元)，之间的一组数据关系见表：
 |
2 |
3 |
4 |
5 |
6 |
 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
已知
，
，
(1)在下面坐标系中画出散点图；
(2)计算
，
，并求出线性回归方程；
(3)在第(2)问条件下，估计该摊主每周7天要是天天出摊，盈利为多少?
某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，其可见部分如下，据此解答如下问题：
（1）计算频率分布直方图中[80,90)间的矩形的高；
（2）若要从分数在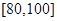
之间的试卷中任取两份分析学生失分情况，求在抽取的试卷中，至少有一份试卷的分数在
之间的概率；
（3）根据频率分布直方图估计这次测试的平均成绩．
粤公网安备 44130202000953号
