福建省高三高考压轴文科数学试卷
设全集U ={1,2,3,4,5},集合A={2,3,4},集合B={3,5},则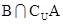 =( )
=( )
| A.{5} | B.{1,2,3,4,5} | C.{1,3,5} | D.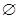 |
已知命题 :$
:$ ,
,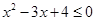 ,则下列说法正确的是( )
,则下列说法正确的是( )
A. :$ :$ , , ,且 ,且 为假命题 为假命题 |
B. :$ :$ , , ,且 ,且 为真命题 为真命题 |
C. :" :" , , ,且 ,且 为假命题 为假命题 |
D. :" :" , , ,且 ,且 为真命题 为真命题 |
现有四个函数:① ;②
;② ;③
;③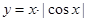 ;④
;④ 的部分图象如下:
的部分图象如下: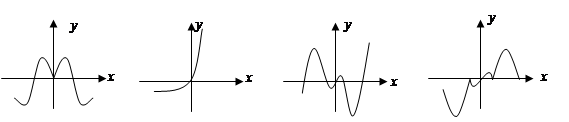
则按照从左到右图象对应的函数序号排列正确的一组是( )
| A.①④②③ | B.①④③② | C.④①②③ | D.③④②① |
若某多面体的三视图(单位: cm)如图所示, 则此多面体的体积是 ( )
A. cm3 cm3 |
B.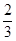 cm3 cm3 |
C.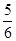 cm3 cm3 |
D.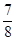 cm3 cm3 |

已知函数 的定义域为
的定义域为 ,若常数
,若常数 满足:对任意正实数
满足:对任意正实数 ,总存在
,总存在 ,使得
,使得 成立,则称
成立,则称 为函数
为函数 的“渐近值”.现有下列三个函数:①
的“渐近值”.现有下列三个函数:①  ;②
;②  ;③
;③  .其中以数“1”为渐近值的函数个数为( )
.其中以数“1”为渐近值的函数个数为( )
| A.0 | B.1 | C.2 | D.3 |
某校有高中学生2000人,其中高三学生800人,高一学生的人数与高二学生人数之比为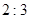 ,为了解高中学生身体素质,采用分层抽样,共抽取一个100人的样本,则样本中高一学生人数为______人.
,为了解高中学生身体素质,采用分层抽样,共抽取一个100人的样本,则样本中高一学生人数为______人.
设 是已知的平面向量,向量
是已知的平面向量,向量 ,
, ,
, 在同一平面内且两两不共线,有如下四个命题:
在同一平面内且两两不共线,有如下四个命题:
①给定向量 ,总存在向量
,总存在向量 ,使
,使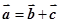 ;
;
②给定向量 和
和 ,总存在实数
,总存在实数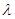 和
和 ,使
,使 ;
;
③给定单位向量 和正数
和正数 ,总存在单位向量
,总存在单位向量 和实数
和实数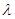 ,使
,使 ;
;
④若 =2,存在单位向量
=2,存在单位向量 、
、 和正实数
和正实数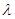 ,
, ,使
,使 ,则
,则
其中真命题是____________.
某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,其可见部分如下,据此解答如下问题:


(1)计算频率分布直方图中[80,90)间的矩形的高;
(2)若要从分数在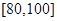 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份试卷的分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份试卷的分数在 之间的概率;
之间的概率;
(3)根据频率分布直方图估计这次测试的平均成绩.
已知实数 ,且
,且 按某种顺序排列成等差数列.
按某种顺序排列成等差数列.
(1)求实数 的值;
的值;
(2)若等差数列 的首项和公差都为
的首项和公差都为 ,等比数列
,等比数列 的首项和公比都为
的首项和公比都为 ,数列
,数列 和
和 的前
的前 项和分别为
项和分别为 ,且
,且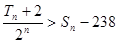 ,求满足条件的自然数
,求满足条件的自然数 的最大值.
的最大值.
已知椭圆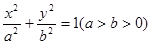 的左右顶点分别为
的左右顶点分别为 ,离心率
,离心率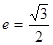 .
.
(1)求椭圆的方程;
(2)若点 为曲线
为曲线 :
: 上任一点(
上任一点( 点不同于
点不同于 ),直线
),直线 与直线
与直线 交于点
交于点 ,
, 为线段
为线段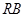 的中点,试判断直线
的中点,试判断直线 与曲线
与曲线 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
 =( )
=( )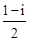



 , 且
, 且 , 则
, 则 ( )
( )

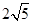
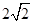
 的值的一个程序框图,其中判断框内应填入的条件是( )
的值的一个程序框图,其中判断框内应填入的条件是( )




 经过坐标原点,且与圆
经过坐标原点,且与圆 相切,切点在第四象限,则直线
相切,切点在第四象限,则直线



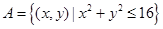 和集合
和集合 表示的平面区域分别为
表示的平面区域分别为 ,若在区域
,若在区域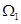 内任取一点
内任取一点 ,则点M落在区域
,则点M落在区域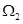 的概率为( )
的概率为( )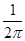



 满足约束条件
满足约束条件 且
且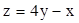 的最大值为
的最大值为 ,最小值为b,则
,最小值为b,则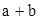 的值是( )
的值是( )
 的一条渐近线与函数
的一条渐近线与函数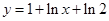 的图象相切,则双曲线
的图象相切,则双曲线 的离心率等于( )
的离心率等于( )




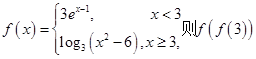 的值为__________.
的值为__________.
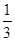 ,则
,则 .
. ,
, 为圆柱
为圆柱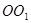 的母线,
的母线, 是底面圆
是底面圆 的直径,
的直径,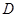 ,
, 分别是
分别是 的中点,
的中点,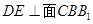 .
. ;
; ;
; 内会有被捕的危险,求鱼被捕的概率.
内会有被捕的危险,求鱼被捕的概率.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号