陕西省宝鸡市金台区高一下学期期末考试数学试卷
算法共有三种逻辑结构,即顺序结构、条件结构和循环结构,下列说法正确的是( ☆ )
| A.一个算法只含有一种逻辑结构 |
| B.一个算法最多可以包含两种逻辑结构 |
| C.一个算法必须含有上述三种逻辑结构 |
| D.一个算法可以含有上述三种逻辑结构 |
从学号为1号至50号的高一某班50名学生中随机选取5名同学参加数学测试,采用系统抽样的
方法,所选5名学生的学号可能是
| A.1,2,3,4,5 | B.5,15,25,35,45 |
| C.2,4,6,8,10 | D.4,13,22,31,40 |
在抽查某产品尺寸的过程中,将其尺寸分成若干组,[12.025,12.045]是其中一组,抽查出的
个数在该组上的频率为 ,则该组上的直方图的高
,则该组上的直方图的高 为
为
A. |
B. |
C. |
D. |
给出以下四个问题:
①输入一个数 ,输出它的相反数;
,输出它的相反数;
②求面积为 的正方形的周长;
的正方形的周长;
③求三个数 中的最大数;
中的最大数;
④求函数 的函数值.
的函数值.
其中不需要用条件语句来描述其算法的有
A. 个 个 |
B. 个 个 |
C. 个 个 |
D. 个 个 |
在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88.若B样本数据恰好是A样本数据每个都加2后所得数据.则A,B两样本的下列数字特征对应相同的是
| A.众数 | B.平均数 | C.中位数 | D.标准差 |
据人口普查统计,育龄妇女生男生女是等可能的,如果允许生育二胎,则某一育龄妇女两胎均
是女孩的概率是
A. |
B. |
C. |
D. |
给出如下四对事件:
①某人射击1次,“射中7环”与“射中8环”;
②甲、乙两人各射击1次,“甲射中7环”与“乙射中8环”;
③甲、乙两人各射击1次,“两人均射中目标”与“两人均没有射中目标”;
④甲、乙两人各射击1次,“至少有1人射中目标”与“甲射中,但乙未射中目标”,
其中属于互斥事件的有
| A.1对 | B.2对 | C.3对 | D.4对 |
以下茎叶图记录了甲、乙两组各五名学生在一次体育测试的成绩(单位:分).已知甲组数据的
中位数为15,乙组数据的平均数为16.8,则 的值分别为
的值分别为
| A.5,8 | B.5,5 | C.2,5 | D.8,8 |
从正方形四个顶点及其中心这5个点中,任取2个点,则这2个点的距离不小于该正方形边长的概率为
A. |
B. |
C. |
D. |
根据如下样本数据得到的回归方程为 ,则
,则
 |
3 |
4 |
5 |
6 |
7 |
8 |
 |
 |
 |
 |
 |
 |
 |
A. ,
, B.
B. ,
, C.
C. ,
, D.
D. ,
,
一个样本a,3,5,7的平均数是b,且a、b是方程 的两根,则这个样本的方
的两根,则这个样本的方
差是________.
(本小题满分17分)某小区每月向居民收取卫生费,计费方法是:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元.设计一个算法,根据输入的人数,计算应收取的卫生费,并画出程序框图.
某班100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;

(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数.
| 分数段 |
[50,60) |
[60,70) |
[70,80) |
[80,90) |
| x∶y |
1∶1 |
2∶1 |
3∶4 |
4∶5 |
(本小题满分18分)某位同学进行寒假社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了1月11日至1月15日的白天平均气温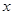 (°C)与该奶茶店的这种饮料销量
(°C)与该奶茶店的这种饮料销量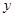 (杯),得到如下数据:
(杯),得到如下数据:
| 日 期 |
1月11日 |
1月12日 |
1月13日 |
1月14日 |
1月15日 |
平均气温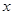 (°C) (°C) |
9 |
10 |
12 |
11 |
8 |
销量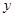 (杯) (杯) |
23[] |
25 |
30 |
26 |
21 |
(1)若从这五组数据中随机抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出y关于x的线性回归方程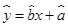 .
.
(参考公式: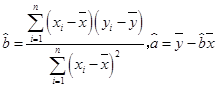 .)
.)




 ,则输出的
,则输出的 值属于( ☆ )
值属于( ☆ )




 输入
输入 ;(
;(
 ;
;
 ;
;
 ;
; 输出
输出 和
和 内任取一个实数,依次记为
内任取一个实数,依次记为 和
和 ,则
,则 的概率为______.
的概率为______.
 和
和 两种型号,某月的产量(单位:个)如下表所示:
两种型号,某月的产量(单位:个)如下表所示:

 的样本,从这个样本中任取
的样本,从这个样本中任取 个杯子,求至少
个杯子,求至少 个
个 粤公网安备 44130202000953号
粤公网安备 44130202000953号