已知数列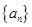 为等差数列,
为等差数列,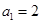 ,
,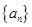 的前
的前 和为
和为 ,数列
,数列 为等
为等
比数列,且 对任意的
对任意的 恒成立.
恒成立.
(Ⅰ)求数列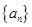 、
、 的通项公式;
的通项公式;
(Ⅱ)是否存在非零整数 ,使不等式
,使不等式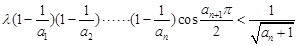 对一切
对一切 都成立?若存在,求出
都成立?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(Ⅲ)各项均为正整数的无穷等差数列 ,满足
,满足 ,且存在正整数k,使
,且存在正整数k,使 成等比数列,若数列
成等比数列,若数列 的公差为d,求d的所有可能取值之和.
的公差为d,求d的所有可能取值之和.
已知数列{an}是等比数列,首项a1=1,公比q>0,其前n项和为Sn,且 成等差数列.
成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足an+1= ,Tn为数列{bn}的前n项和,若Tn≥m恒成立,求m的最大值.
,Tn为数列{bn}的前n项和,若Tn≥m恒成立,求m的最大值.
已知数列 是递增的等比数列,满足
是递增的等比数列,满足 ,且
,且 是
是 .
. 的等差中项,数列
的等差中项,数列 满足
满足 ,其前n项和为
,其前n项和为 ,且
,且 .
.
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)数列 的前n项和为
的前n项和为 ,若不等式
,若不等式 对一切
对一切 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知点 (
( )满足
)满足 ,
, ,且点
,且点 的坐标为
的坐标为  .
.
(1)求经过点 的直线
的直线 的方程;
的方程;
(2)已知点 (
( )在
)在 两点确定的直线
两点确定的直线 上,求证:数列
上,求证:数列 是等差数列;
是等差数列;
(3)在(2)的条件下,求对于所有 ,能使不等式
,能使不等式 成立的最大实数
成立的最大实数 的值.
的值.