等差数列{an}的各项均为正数,a1=3,前n项和为Sn,{bn}为等比数列,b1=1,且b2S2=64,b3S3=960.
(1)求an与bn;
(2)求 +
+ +…+
+…+ .
.
设等差数列 的前
的前 项和为
项和为 ,
, 数列
数列 的前
的前 项和为
项和为 满足
满足
(Ⅰ)求数列 的通项公式及数列
的通项公式及数列 的前
的前 项和;
项和;
(Ⅱ)是否存在非零实数 ,使得数列
,使得数列 为等比数列?并说明理由
为等比数列?并说明理由
已知等差数列 的公差为
的公差为 ,前
,前 项和为
项和为 ,且
,且 .
.
(Ⅰ)求数列 的通项公式
的通项公式 与前
与前 项和
项和 ;
;
(Ⅱ)从数列 的前五项中抽取三项按原来顺序恰为等比数列
的前五项中抽取三项按原来顺序恰为等比数列 的前三项,记数列
的前三项,记数列 的前
的前 项和为
项和为 ,若存在
,若存在 ,使得对任意
,使得对任意 ,总有
,总有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
已知数列 为等差数列,
为等差数列, ,其前
,其前 和为
和为 ,数列
,数列 为等比数列,且
为等比数列,且 对任意的
对任意的 恒成立.
恒成立.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)是否存在 ,使得
,使得 成立,若存在,求出所有满足条件的
成立,若存在,求出所有满足条件的 ;若不存在,说明理由.
;若不存在,说明理由.
已知由整数组成的数列 各项均不为0,其前n项和为 ,且
各项均不为0,其前n项和为 ,且
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的通项公式;
的通项公式;
(Ⅲ)若 时,
时, 取得最小值,求a的值.
取得最小值,求a的值.
已知数列{ }是公差不为0的等差数列,a1=2且a2, a3, a4+1成等比数列.
}是公差不为0的等差数列,a1=2且a2, a3, a4+1成等比数列.
(1)求数列{ }的通项公式;
}的通项公式;
(2)设 ,求数列{
,求数列{ }的前n项和
}的前n项和
(本题满分18分,第1小题满分4分,第2小题满分6分,第3小题满分8分.)
已知数列{ }满足:
}满足: ,
, 为数列
为数列 的前
的前 项和。
项和。
(1)若{ }是递增数列,且
}是递增数列,且 成等差数列,求
成等差数列,求 的值;
的值;
(2)若 ,且{
,且{ }是递增数列,{
}是递增数列,{ }是递减数列,求数列{
}是递减数列,求数列{ }的通项公式;
}的通项公式;
(3)若 ,对于给定的正整数
,对于给定的正整数 ,是否存在一个满足条件的数列
,是否存在一个满足条件的数列 ,使得
,使得 ,如果存在,给出一个满足条件的数列,如果不存在,请说明理由。
,如果存在,给出一个满足条件的数列,如果不存在,请说明理由。
(本题满分18分,第1小题满分4分,第2小题满分6分,第3小题满分8分.)
已知数列{ }满足:
}满足: ,
, 为数列
为数列 的前
的前 项和。
项和。
(1)若{ }是递增数列,且
}是递增数列,且 成等差数列,求
成等差数列,求 的值;
的值;
(2)若 ,且{
,且{ }是递增数列,{
}是递增数列,{ }是递减数列,求数列{
}是递减数列,求数列{ }的通项公式;
}的通项公式;
(3)若 ,对于给定的正整数
,对于给定的正整数 ,是否存在一个满足条件的数列
,是否存在一个满足条件的数列 ,使得
,使得 ,如果存在,给出一个满足条件的数列,如果不存在,请说明理由。
,如果存在,给出一个满足条件的数列,如果不存在,请说明理由。
(本小题满分12分)
已知等差数列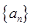 的公差为
的公差为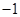 ,前
,前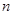 项和为
项和为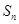 ,且
,且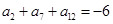 .
.
(1)求数列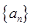 的通项公式
的通项公式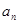 与前
与前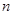 项和
项和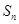 ;
;
(2)将数列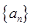 的前四项抽取其中一项后,剩下三项按原来顺序恰为等比数列
的前四项抽取其中一项后,剩下三项按原来顺序恰为等比数列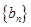 的前三项,记数列
的前三项,记数列 的前
的前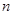 项和为
项和为 ,若存在
,若存在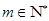 ,使得对任意
,使得对任意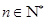 ,总有
,总有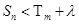 成立,求实数
成立,求实数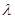 的取值范围.
的取值范围.