(本小题共12分)对于数列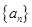 ,定义其积数是
,定义其积数是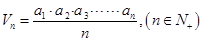 .
.
(1)若数列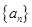 的积数是
的积数是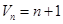 ,求
,求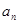 ;
;
(2)等比数列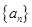 中,
中,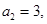
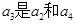 的等差中项,若数列
的等差中项,若数列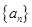 的积数
的积数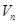 满足
满足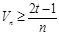 对一切
对一切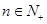 恒成立,求实数
恒成立,求实数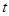 的取值范围.
的取值范围.
(本小题满分12分)等差数列 中,
中, ,其前
,其前 项和为
项和为 .等比数列
.等比数列 的各项均为正数,
的各项均为正数, ,且
,且 ,
, .
.
(1)求数列 与
与 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 .
.
(本小题满分12分)已知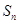 是等差数列
是等差数列 的前n项和,数列
的前n项和,数列 是等比数列,
是等比数列,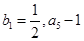 恰为
恰为 的等比中项,圆
的等比中项,圆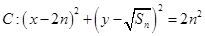 ,直线
,直线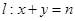 ,对任意
,对任意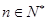 ,直线
,直线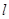 都与圆C相切.
都与圆C相切.
(Ⅰ)求数列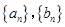 的通项公式;
的通项公式;
(Ⅱ)若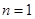 时,
时,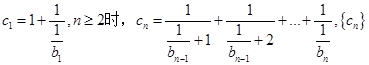 的前n项和为
的前n项和为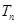 ,求证:对任意
,求证:对任意 ,都有
,都有
(本小题满分12分) 若数列 是等比数列,
是等比数列, ,公比
,公比 ,已知
,已知 和
和 的等差中项为
的等差中项为 ,且
,且 .
.
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项和.
项和.
本题共有3小题,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分8分.
已知数列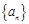 是首项为3,公比为
是首项为3,公比为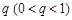 的无穷等比数列,且数列
的无穷等比数列,且数列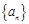 各项的和等于9.对给定的
各项的和等于9.对给定的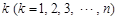 ,设
,设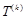 是首项为
是首项为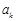 ,公差为
,公差为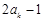 的等差数列.
的等差数列.
(1)求数列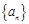 的通项
的通项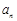 ;
;
(2)求数列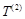 的前10项之和;
的前10项之和;
(3)设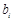 为数列
为数列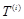 的第
的第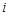 项,
项,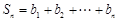 ,求
,求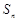 ,并求正整数
,并求正整数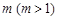 ,使得
,使得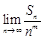 存在且不等于零.
存在且不等于零.
(本小题满分16分)已知数列 的奇数项是首项为
的奇数项是首项为 的等差数列,偶数项是首项为
的等差数列,偶数项是首项为 的等比数列,数列
的等比数列,数列 前
前 项和为
项和为 ,且满足
,且满足 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,求正整数
,求正整数 的值;
的值;
(3)是否存在正整数 ,使得
,使得 恰好为数列
恰好为数列 中的一项?若存在,求出所有满足条件的
中的一项?若存在,求出所有满足条件的 值,若不存在,说明理由.
值,若不存在,说明理由.
(本小题满分16分)设数列 的前
的前 项和为
项和为 ,满足
,满足
 .
.
(1)当 时,
时,
①设 ,若
,若 ,
, .求实数
.求实数 的值,并判定数列
的值,并判定数列 是否为等比数列;
是否为等比数列;
②若数列 是等差数列,求
是等差数列,求 的值;
的值;
(2)当 时,若数列
时,若数列 是等差数列,
是等差数列, ,且
,且 ,
, ,
,
求实数 的取值范围.
的取值范围.
(本小题满分12分)已知正项数列 的首项
的首项 ,前
,前 项和
项和 满足
满足 .
.
(1)求证: 为等差数列,并求数列
为等差数列,并求数列 的通项公式;
的通项公式;
(2)记数列 的前
的前 项和为
项和为 ,若对任意的
,若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知数列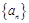 的前n项和为
的前n项和为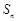 ,设数列
,设数列 满足
满足 .
.
(1)若数列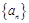 为等差数列,且
为等差数列,且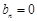 ,求数列
,求数列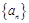 的通项公式;
的通项公式;
(2)若 ,
,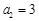 ,且数列
,且数列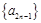 ,
,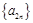 都是以2为公比的等比数列,求满足不等式
都是以2为公比的等比数列,求满足不等式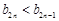 的所有正整数n的集合.
的所有正整数n的集合.
(本题满分16分)本题共3小题,第(1)小题4分,第(2)小题4分,第(3)小题8分.
已知数列 是公差不为
是公差不为 的等差数列,
的等差数列, 数列
数列 是等比数列,且
是等比数列,且 ,
, ,数列
,数列 的前
的前 项和为
项和为 ,记点
,记点 .
.
(1)求数列 的通项公式;
的通项公式;
(2)证明:点 在同一直线
在同一直线 上,并求出直线
上,并求出直线 方程;
方程;
(3)若 对
对 恒成立,求
恒成立,求 的最小值.
的最小值.
已知数列 的前
的前 项和为
项和为 ,且
,且 ,
, N*
N*
(1)求数列 的通项公式;
的通项公式;
(2)已知 (
( N*),记
N*),记
 (
(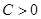 且
且 ),是否存在这样的常数
),是否存在这样的常数 ,使得数列
,使得数列 是常数列,若存在,求出
是常数列,若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)若数列 ,对于任意的正整数
,对于任意的正整数 ,均有
,均有 成立,求证:数列
成立,求证:数列 是等差数列;
是等差数列;