(本小题满分12分)
已知函数 ,
, .
.
(1)若 在
在 上的最大值为
上的最大值为 ,求实数
,求实数 的值;
的值;
(2)若对任意 ,都有
,都有 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)在(1)的条件下,设 ,对任意给定的正实数
,对任意给定的正实数 ,曲线
,曲线 上是否存在两点
上是否存在两点 、
、 ,使得
,使得 是以
是以 (
( 为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在 轴上?请说明理由.
轴上?请说明理由.
(本小题满分12分)
已知等差数列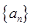 的公差为
的公差为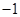 ,前
,前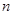 项和为
项和为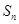 ,且
,且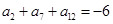 .
.
(1)求数列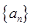 的通项公式
的通项公式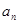 与前
与前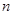 项和
项和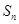 ;
;
(2)将数列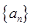 的前四项抽取其中一项后,剩下三项按原来顺序恰为等比数列
的前四项抽取其中一项后,剩下三项按原来顺序恰为等比数列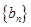 的前三项,记数列
的前三项,记数列 的前
的前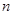 项和为
项和为 ,若存在
,若存在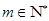 ,使得对任意
,使得对任意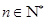 ,总有
,总有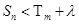 成立,求实数
成立,求实数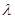 的取值范围.
的取值范围.
(本小题满分12分)
已知椭圆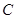 的两个焦点分别为
的两个焦点分别为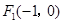 、
、 ,短轴的两个端点分别为
,短轴的两个端点分别为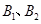 .
.
(Ⅰ)若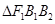 为等边三角形,求椭圆
为等边三角形,求椭圆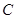 的方程;
的方程;
(Ⅱ)若椭圆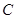 的短轴长为
的短轴长为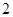 ,过点
,过点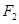 的直线
的直线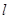 与椭圆
与椭圆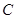 相交于
相交于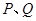 两点,且
两点,且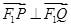 ,
,
求直线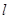 的方程.
的方程.
(本小题满分12分)
已知椭圆 :
: 的离心率为
的离心率为 ,其中左焦点
,其中左焦点 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若直线 与椭圆
与椭圆 交于不同的
交于不同的 两点,且线段
两点,且线段 的中点
的中点 在圆
在圆 上,求
上,求 的值.
的值.
(本小题满分10分)
已知椭圆 的中心在坐标原点,右焦点为
的中心在坐标原点,右焦点为 ,
, 、
、 分别是椭圆
分别是椭圆 的左右顶点,
的左右顶点, 是
是
椭圆 上的动点.
上的动点.
(Ⅰ)若 面积的最大值为
面积的最大值为 ,求椭圆
,求椭圆 的方程;
的方程;
(Ⅱ)过右焦点 做长轴
做长轴 的垂线,交椭圆
的垂线,交椭圆 于
于 、
、 两点,若
两点,若 ,求椭圆
,求椭圆 的
的
离心率.
(本小题满分12分)
已知椭圆 :
: 的离心率为
的离心率为 ,其中左焦点
,其中左焦点 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若直线 与椭圆
与椭圆 交于不同的
交于不同的 两点,且线段
两点,且线段 的中点
的中点 在圆
在圆 上,求
上,求 的值.
的值.
为捍卫钓鱼岛及其附属岛屿的领土主权,中国派出海警“2102”、“海警2307”和“海警2308”海警船编队在钓鱼岛领海巡航。某日,正巡逻在A处的海警“2102”突然发现来自P处的疑似敌舰的某信号,发现信号时“海警2307”和“海警2308”正分别位于如图所示的B、C两处,其中 在
在 的正东方向相距
的正东方向相距 千米处,
千米处, 在
在 的北偏西30°方向相距
的北偏西30°方向相距 千米处。由于
千米处。由于 、
、 比
比 距
距 更远,因此,4秒后
更远,因此,4秒后 、
、 才同时发现这一信号(该信号的传播速度为每秒
才同时发现这一信号(该信号的传播速度为每秒 千米),试确定疑似敌舰相对于A的位置.
千米),试确定疑似敌舰相对于A的位置.
已知函数 ,
, .
.
(1)若 ,求函数
,求函数 的极值;
的极值;
(2)设函数 ,求函数
,求函数 的单调区间;
的单调区间;
(3)若在 上存在一点
上存在一点 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
如图,已知长方形 中,
中, ,
, 为
为 的中点,将
的中点,将 沿
沿 折起,使得平面
折起,使得平面
 平面
平面 .
.
(1)求证: ;
;
(2)若点 是线段
是线段 上的一动点,问点
上的一动点,问点 在何位置时,二面角
在何位置时,二面角 的余弦值为
的余弦值为 .
.
已知函数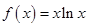 ,
,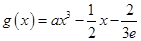 .
.
(1)求 的单调增区间和最小值;
的单调增区间和最小值;
(2)若函数 与函数
与函数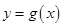 在交点处存在公共切线,求实数
在交点处存在公共切线,求实数 的值;
的值;
(3)若 时,函数
时,函数 的图象恰好位于两条平行直线
的图象恰好位于两条平行直线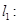
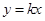 ,
,
 之间,当
之间,当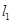 与
与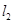 间的距离最小时,求实数
间的距离最小时,求实数 的值.
的值.
已知函数 的图象在点
的图象在点 (
( 为自然对数的底数)处的切线斜率为3.
为自然对数的底数)处的切线斜率为3.
(1)求实数 的值 ;
的值 ;
(2)若 ,且
,且 对任意
对任意 恒成立,求
恒成立,求 最大值;
最大值;
(3)当 时,证明
时,证明 .
.