如图，有一块半椭圆形钢板，其长半轴长为2，短半轴长为1，计划将此钢板切割成等腰梯形的形状，下底AB是半椭圆的短轴，上底CD的端点在椭圆上，记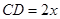
，梯形面积为S．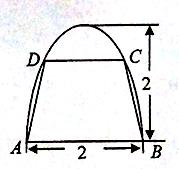
（1）求面积S以x为自变量的函数式，并写出其定义域；
（2）求面积S的最大值．
，
，且
，求
，
的值
，
，
，求
的值．
，
，
求
的值.
,B=
，求实数a的取值范围；
，求实数a的取值范围。
，
，若
，求实数
的取值范围.推荐套卷
如图，有一块半椭圆形钢板，其长半轴长为2，短半轴长为1，计划将此钢板切割成等腰梯形的形状，下底AB是半椭圆的短轴，上底CD的端点在椭圆上，记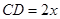，梯形面积为S．
（1）求面积S以x为自变量的函数式，并写出其定义域；
（2）求面积S的最大值．
粤公网安备 44130202000953号