已知点 是圆
是圆 上任意一点,过点
上任意一点,过点 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,点
,点 满足
满足 记点
记点 的轨迹为曲线
的轨迹为曲线 .
.
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)设 ,点
,点 在曲线
在曲线 上,且直线
上,且直线 与直线
与直线 的斜率之积为
的斜率之积为 ,求
,求 的面积的最大值.
的面积的最大值.
(本题14分)已知椭圆 的方程为
的方程为 ,称圆心在坐标原点
,称圆心在坐标原点 ,半径为
,半径为
的圆为椭圆 的“伴随圆”,椭圆
的“伴随圆”,椭圆 的短轴长为2,离心率为
的短轴长为2,离心率为 .
.
(1)求椭圆 及其“伴随圆”的方程;
及其“伴随圆”的方程;
(2)若直线 与椭圆
与椭圆 交于
交于 两点,与其“伴随圆”交于
两点,与其“伴随圆”交于 两点,当
两点,当  时,求△
时,求△ 面积
面积
的最大值.
(本小题满分16分)已知函数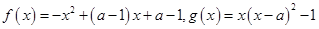 ,其中a为实数.
,其中a为实数.
(1)是否存在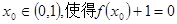 ?若存在,求出实数a的取值范围;若不存在,请说明理由.
?若存在,求出实数a的取值范围;若不存在,请说明理由.
(2)若集合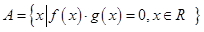 中恰有5个元素,求实数a的取值范围.
中恰有5个元素,求实数a的取值范围.
设正项数列{an}(n≥5)对任意正整数k(k≥3)恒满足: ,且
,且 .
.
(1)求数列{an}的通项公式;
(2)是否存在整数 ,使得
,使得 对于任意正整数n恒成立?若存在,求出
对于任意正整数n恒成立?若存在,求出 的值;若不存在,说明理由。(注:
的值;若不存在,说明理由。(注: )
)
(附加题,本小题满分10分,该题计入总分)数列{ }的前
}的前 项和为
项和为 ,
, 是
是 和
和 的等差中项,等差数列{
的等差中项,等差数列{ }满足
}满足 ,
, .
.
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列 的前
的前 项和
项和
(附加题,本小题满分10分,该题计入总分)已知数列 的前
的前 项和
项和 ,且
,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)令 ,是否存在
,是否存在 ,使得
,使得 成等比数列.若存在,求出所有符合条件的
成等比数列.若存在,求出所有符合条件的 值;若不存在,请说明理由.
值;若不存在,请说明理由.
(本小题满分12分)已知在直角坐标系 中,圆锥曲线
中,圆锥曲线 的参数方程为
的参数方程为 (
( 为参数),定点
为参数),定点 ,
, 是圆锥曲线
是圆锥曲线 的左、右焦点.
的左、右焦点.
(Ⅰ)以坐标原点为极点, 轴正半轴为极轴建立极坐标系,求经过点
轴正半轴为极轴建立极坐标系,求经过点 且平行于直线
且平行于直线 的直线
的直线 的极坐标方程;
的极坐标方程;
(Ⅱ)设(Ⅰ)中直线 与圆锥曲线
与圆锥曲线 交于
交于 两点,求
两点,求 .
.
(本小题满分13分)2008年5月12日14时28分04秒,四川省阿坝藏族羌族自治州汶川县发生里氏8.0级地震,地震造成69227人遇难,374643人受伤,17923人失踪。重庆众多医务工作者和志愿者加入了抗灾救援行动。其中重庆三峡中心医院外科派出由5名骨干医生组成的救援小组,奔赴受灾第一线参与救援。现将这5名医生分别随机分配到受灾最严重的汶川县、北川县、绵竹三县中的某一个。
(1)求每个县至少分配到一名医生的概率。
(2)若将随机分配到汶川县的人数记为 ,求随机变量
,求随机变量 的分布列,期望和方差。
的分布列,期望和方差。
(本题满分为15分)如图,已知长方形 中,
中, ,
, 为
为 的中点.将
的中点.将 沿
沿 折起,使得平面
折起,使得平面 平面
平面 .
.

(1)求证: ;
;
(2)若点 是线段
是线段 上的一动点,问点E在何位置时,二面角
上的一动点,问点E在何位置时,二面角 的余弦值为
的余弦值为 .
.
(1)若 的展开式中,
的展开式中, 的系数是
的系数是 的系数的
的系数的 倍,求
倍,求 ;
;
(2)已知 的展开式中,
的展开式中,  的系数是
的系数是 的系数与
的系数与 的系数的等差中项,求
的系数的等差中项,求 ;
;
(3)已知 的展开式中,二项式系数最大的项的值等于
的展开式中,二项式系数最大的项的值等于 ,求
,求 .
.