从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
| 质量指标 值分组 |
[75,85) |
[85,95) |
[95,105) |
[105,115) |
[115,125) |
| 频数 |
6 |
26 |
38 |
22 |
8 |
(Ⅰ)在答题卡上列出这些数据频率分布表,并作出频率分布直方图;
(Ⅱ)估计这种产品质量指标值的平均值及方差(同一组中的数据用该组区间的中点值作代表).
给出下列结论:
①扇形的圆心角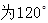 ,半径为2,则扇形的弧长
,半径为2,则扇形的弧长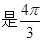 ;
;
②某小礼堂有25排座位,每排20个,一次心理学讲座,礼堂中坐满了学生,会后为了了解有关情况,留下座位号是15的所有25名学生进行测试,这里运用的是系统抽样方法;
③一个人打靶时连续射击两次,则事件“至少有一次中靶”与事件“两次都不中靶”互为对立事件;
④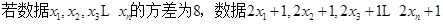
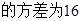 ;
;
⑤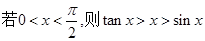 .
.
其中正确结论的序号为 .(把你认为正确结论的序号都填上).
有五条线段,长度分别为1,3,5,7,9.从这五条线段中任取三条,则所取三条线段不能构成一个三角形的概率为
A.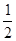 |
B.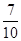 |
C.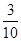 |
D.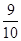 |
(本小题满分14分)函数 ,(
,( )的最小正周期为
)的最小正周期为 ,且在
,且在 处取得最小值
处取得最小值 .
.
(Ⅰ)求 的单调递增区间;
的单调递增区间;
(Ⅱ)将 的图象向左平移
的图象向左平移 个单位后得到函数
个单位后得到函数 ,设
,设 为三角形的三个内角,若
为三角形的三个内角,若 ,且
,且 ,求
,求 的取值范围.
的取值范围.
(本小题满分13分)如图: 是直径为
是直径为 的半圆,
的半圆, 为圆心,
为圆心, 是
是 上一点,且
上一点,且 .
. ,且
,且 ,
, ,
, 为
为 的中点,
的中点, 为
为 的中点,
的中点, 为
为 上一点,且
上一点,且 .
.
(Ⅰ)求证: 面 ⊥面
⊥面 ;
;
(Ⅱ)求证: ∥平面
∥平面 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
(本小题满分12分)如图,两同心圆(圆心在原点)分别与 、
、 交于
交于 、
、 两点,其中
两点,其中 ,
, ,阴影部分为两同心圆构成的扇环,已知扇环的面积为
,阴影部分为两同心圆构成的扇环,已知扇环的面积为 .
.
(Ⅰ)设角 的始边为
的始边为 轴的正半轴,终边为
轴的正半轴,终边为 ,求
,求 的值;
的值;
(Ⅱ)求点 的坐标.
的坐标.
某校共有学生2000名,各年级男、女生人数如表.已知在全校学生中随机抽取1名,抽到二年级女生的概率是0.19.现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为
| |
一年级 |
二年级 |
三年级 |
| 女生 |
373 |
x |
y |
| 男生 |
377 |
370 |
z |
A.24 B.18 C.16 D.12