函数y=ax2+bx+c的图象如图所示,那么关于x的一元二次方程ax2+bx+c﹣4=0的根的情况是( )

| A.有两个不相等的实数根 |
| B.有两个异号的实数根 |
| C.有两个相等的实数根 |
| D.没有实数根 |
下表是某一天河南省8个城市的最高气温预报,则这8个市的最高气温的众数与中位数分别是( )
| 城市 |
郑州 |
洛阳 |
开封 |
安阳 |
新乡 |
焦作 |
南阳 |
商丘 |
| 最高气温(℃) |
16 |
11 |
17 |
13 |
11 |
13 |
9 |
11 |
A.11, 13 B.11, 12.5 C.11, 12 D.13, 12
(本小题满分12分)设 的内角
的内角 所对的边分别为
所对的边分别为 且
且 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,求
,求 的周长
的周长 的取值范围.
的取值范围.
(本小题满分12分)已知 .
.
(Ⅰ)当 时,解不等式
时,解不等式 ;
;
(Ⅱ)若 ,解关于x的不等式
,解关于x的不等式 .
.
(本小题满分12分)某制造商3月生产了一批乒乓球,从中随机抽样100个进行检查,测得每个球的直径(单位:mm),将数据分组如下:
| 分组 |
频数 |
频率 |
| [39.95,39.97) |
10 |
|
| [39. 97,39.99) |
20 |
|
| [39.99,40.01) |
50 |
|
| [40.01,40.03] |
20 |
|
| 合计 |
100 |
|

(Ⅰ)请在上表中补充完成频率分布表(结果保留两位小数),并在图中画出频率分布直方图;
(Ⅱ)若以上述频率作为概率,已知标准乒乓球的直径为40.00 mm,试求这批球的直径误差不超过0.03 mm的概率;
(Ⅲ)统计方法中,同一组数据经常用该组区间的中点值(例如区间[39.99,40.01)的中点值是40.00作为代表.据此估计这批乒乓球直径的平均值(结果保留两位小数).
(共12分)已知函数 直线
直线 是
是 图像的任意两条对称轴,且
图像的任意两条对称轴,且 的最小值为
的最小值为 .
.
(1)求函数 的单调增区间;
的单调增区间;
(2)求使不等式 的
的 的取值范围.
的取值范围.
(3)若 求
求 的值;
的值;
已知函数f(x)是定义在R上不恒为零的函数,且对于任意实数a,b∈R,满足:
 (ab)=a
(ab)=a (b)+b
(b)+b (a),
(a), (2)=2,an=
(2)=2,an= (n∈N*),bn=
(n∈N*),bn= (n∈N*).
(n∈N*).
考察下列结论:
① (0)=
(0)= (1);
(1);
② (x)为偶函数;
(x)为偶函数;
③数列{an}为等比数列;
④数列{bn}为等差数列.
其中正确的结论共有 .
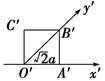
如图,一个平面图形的斜二测画法的直观图是一个边长为a的正方形,则原平面图形的面积为( )
A.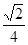 a2 a2 |
B.a2 | C.2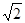 a2 a2 |
D.2a2 |
(本小题满分12分)在 中,已知点
中,已知点 为线段
为线段 上的一点,且
上的一点,且 .
.
(1)试用 表示
表示 ;
;
(2)若 ,且
,且 ,求
,求 的值.
的值.
(本小题12分)已知sin(2α-β)=  ,sinβ=" -"
,sinβ=" -"  ,且α∈(
,且α∈( ,π),β∈(-
,π),β∈(- ,0),求sinα的值.
,0),求sinα的值.