初中数学解直角三角形的应用-仰角俯角问题试题

我国航天事业捷报频传，天舟二号于2021年5月29日成功发射，震撼人心．当天舟二号从地面到达点 $A$ 处时，在 $P$ 处测得 $A$ 点的仰角 $\angle \mathit{DPA}$ 为 $30°$ 且 $A$ 与 $P$ 两点的距离为6千米，它沿铅垂线上升7.5秒后到达 $B$ 处，此时在 $P$ 处测得 $B$ 点的仰角 $\angle \mathit{DPB}$ 为 $45°$ ，求天舟二号从 $A$ 处到 $B$ 处的平均速度．（结果精确到 $1m/s$ ，取 $\sqrt{3}=1.732$ ， $\sqrt{2}=1.414)$

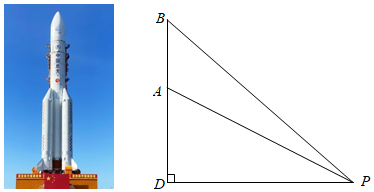
政府将要在某学校大楼前修一座大桥．如图，宋老师测得大楼的高是20米，大楼的底部 $D$ 处与将要修的大桥 $\mathit{BC}$ 位于同一水平线上，宋老师又上到楼顶 $A$ 处测得 $B$ 和 $C$ 的俯角 $\angle \mathit{EAB}$ ， $\angle \mathit{EAC}$ 分别为 $67°$ 和 $22°$ ，宋老师说现在我能算出将要修的大桥 $\mathit{BC}$ 的长了．同学们：你知道宋老师是怎么算的吗？请写出计算过程（结果精确到0.1米）．

其中 $\sin 67°\approx \frac{12}{13}$ ， $\cos 67°\approx \frac{5}{13}$ ， $\tan 67°\approx \frac{12}{5}$ ， $\sin 22°\approx \frac{3}{8}$ ， $\cos 22°\approx \frac{15}{16}$ ， $\tan 22°\approx \frac{2}{5}$

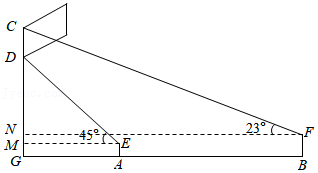
今年是建党100周年，学校新装了国旗旗杆（如图所示），星期一该校全体学生在国旗前举行了升旗仪式．仪式结束后，站在国旗正前方的小明在 $A$ 处测得国旗 $D$ 处的仰角为 $45°$ ，站在同一队列 $B$ 处的小刚测得国旗 $C$ 处的仰角为 $23°$ ，已知小明目高 $\mathit{AE}=1.4$ 米，距旗杆 $\mathit{CG}$ 的距离为15.8米，小刚目高 $\mathit{BF}=1.8$ 米，距小明24.2米，求国旗的宽度 $\mathit{CD}$ 是多少米？（最后结果保留一位小数）

（参考数据： $\sin 23°\approx 0.3907$ ， $\cos 23°\approx 0.9205$ ， $\tan 23°\approx 0.4245)$

如图，建筑物 $\mathit{BC}$上有一旗杆 $\mathit{AB}$，从与 $\mathit{BC}$相距 $20m$的 $D$处观测旗杆顶部 $A$的仰角为 $52°$，观测旗杆底部 $B$的仰角为 $45°$，求旗杆 $\mathit{AB}$的高度（结果保留小数点后一位．参考数据： $\sin 52°\approx 0.79$， $\cos 52°\approx 0.62$， $\tan 52°\approx 1.28$， $\sqrt{2}\approx 1.41)$．

如图，小明利用一个锐角是 $30°$ 的三角板测操场旗杆的高度，已知他与旗杆之间的水平距离 $\mathit{BC}$ 为 $15m$ ， $\mathit{AB}$ 为 $1.5m$ （即小明的眼睛与地面的距离），那么旗杆的高度是 $($ 　　 $)$

A．

$(15\sqrt{3}+\frac{3}{2})m$

B．

$5\sqrt{3}m$

C．

$15\sqrt{3}m$

D．

$(5\sqrt{3}+\frac{3}{2})m$

如图，直立于地面上的电线杆 $\mathit{AB}$，在阳光下落在水平地面和坡面上的影子分别是 $\mathit{BC}$、 $\mathit{CD}$，测得 $\mathit{BC}=5$米， $\mathit{CD}=4$米， $\angle \mathit{BCD}=150°$，在 $D$处测得电线杆顶端 $A$的仰角为 $45°$，则电线杆 $\mathit{AB}$的高度约为 　　米．

（参考数据： $\sqrt{2}\approx 1.414$， $\sqrt{3}\approx 1.732$，结果按四舍五入保留一位小数）

如图，建筑物 $\mathit{BC}$上有一高为 $8m$的旗杆 $\mathit{AB}$，从 $D$处观测旗杆顶部 $A$的仰角为 $53°$，观测旗杆底部 $B$的仰角为 $45°$，则建筑物 $\mathit{BC}$的高约为　　 $m$（结果保留小数点后一位）．（参考数据： $\sin 53°\approx 0.80$， $\cos 53°\approx 0.60$， $\tan 53\approx 1.33)$

乡村振兴使人民有更舒适的居住条件，更优美的生活环境，如图是怡佳新村中的两栋居民楼，小明在甲居民楼的楼顶 $D$处观测乙居民楼楼底 $B$处的俯角是 $30°$，观测乙居民楼楼顶 $C$处的仰角为 $15°$，已知甲居民楼的高为 $10m$，求乙居民楼的高．（参考数据： $\sqrt{2}\approx 1.414$， $\sqrt{3}\approx 1.732$，结果精确到 $0.1m)$

开凿于北魏孝文帝年间的龙门石窟是中国石刻艺术瑰宝，卢舍那佛像是石窟中最大的佛像．某数学活动小组到龙门石窟景区测量这尊佛像的高度．如图，他们选取的测量点 $A$与佛像 $\mathit{BD}$的底部 $D$在同一水平线上．已知佛像头部 $\mathit{BC}$为 $4m$，在 $A$处测得佛像头顶部 $B$的仰角为 $45°$，头底部 $C$的仰角为 $37.5°$，求佛像 $\mathit{BD}$的高度（结果精确到 $0.1m$．参考数据： $\sin 37.5°\approx 0.61$， $\cos 37.5°\approx 0.79$， $\tan 37.5°\approx 0.77)$．

如图，在某信号塔 $\mathit{AB}$的正前方有一斜坡 $\mathit{CD}$，坡角 $\angle \mathit{CDK}=30°$，斜坡的顶端 $C$与塔底 $B$的距离 $\mathit{BC}=8$米，小明在斜坡上的点 $E$处测得塔顶 $A$的仰角 $\angle \mathit{AEN}=60°$， $\mathit{CE}=4$米，且 $\mathit{BC}//\mathit{NE}//\mathit{KD}$， $\mathit{AB}\perp \mathit{BC}$（点 $A$， $B$， $C$， $D$， $E$， $K$， $N$在同一平面内）．

（1）填空： $\angle \mathit{BCD}=$　　度， $\angle \mathit{AEC}=$　　度；

（2）求信号塔的高度 $\mathit{AB}$（结果保留根号）．

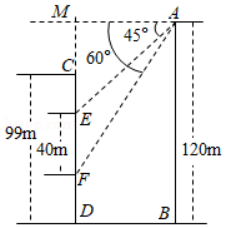
如图，在一座山的前方有一栋住宅，已知山高 $\mathit{AB}=120m$ ，楼高 $\mathit{CD}=99m$ ，某天上午9时太阳光线从山顶点 $A$ 处照射到住宅的点 $E$ 外．在点 $A$ 处测得点 $E$ 的俯角 $\angle \mathit{EAM}=45°$ ，上午10时太阳光线从山顶点 $A$ 处照射到住宅点 $F$ 处，在点 $A$ 处测得点 $F$ 的俯角 $\angle \mathit{FAM}=60°$ ，已知每层楼的高度为 $3m$ ， $\mathit{EF}=40m$ ，问：以当天测量数据为依据，不考虑季节天气变化，至少要买该住宅的第几层楼，才能使上午10时太阳光线照射到该层楼的外墙？ $(\sqrt{3}\approx 1.73)$

随着科学技术的不断进步，无人机被广泛应用到实际生活中，小星利用无人机来测量广场 $B$， $C$两点之间的距离．如图所示，小星站在广场的 $B$处遥控无人机，无人机在 $A$处距离地面的飞行高度是 $41.6m$，此时从无人机测得广场 $C$处的俯角为 $63°$，他抬头仰视无人机时，仰角为 $\alpha$，若小星的身高 $\mathit{BE}=1.6m$， $\mathit{EA}=50m$（点 $A$， $E$， $B$， $C$在同一平面内）．

（1）求仰角 $\alpha$的正弦值；

（2）求 $B$， $C$两点之间的距离（结果精确到 $1m)$．

$(\sin 63°\approx 0.89$， $\cos 63°\approx 0.45$， $\tan 63°\approx 1.96$， $\sin 27°\approx 0.45$， $\cos 27°\approx 0.89$， $\tan 27°\approx 0.51)$

如图，垂直于水平面的 $5G$ 信号塔 AB建在垂直于水平面的悬崖边 B点处，某测量员从山脚 C点出发沿水平方向前行78米到 D点（点 A， B， C在同一直线上），再沿斜坡 $\mathit{DE}$ 方向前行78米到 E点（点 A， B， C， D， E在同一平面内），在点 E处测得 $5G$ 信号塔顶端 A的仰角为43°，悬崖 BC的高为144.5米，斜坡 DE的坡度（或坡比） $i＝1：2.4$ ，则信号塔 AB的高度约为（　　）

（参考数据： $\mathit{sin}43°\approx 0.68$ ， $\mathit{cos}43°\approx 0.73$ ， $\mathit{tan}43°\approx 0.93$ ）

A．

23米

B．

24米

C．

24.5米

D．

25米

如图，数学活动小组利用测角仪和皮尺测量学校旗杆的高度，在点D处测得旗杆顶端A的仰角 $\angle \mathit{ADE}为55°$，测角仪CD的高度为1米，其底端C与旗杆底端B之间的距离为6米，设旗杆AB的高度为x米，则下列关系式正确的是（　　）

A． $\mathit{tan}55°=\frac{6}{x-1}$B． $\mathit{tan}55°=\frac{x-1}{6}$

C． $\sin 55°=\frac{x-1}{6}$D． $\cos 55°=\frac{x-1}{6}$

某校“综合与实践”小组采用无人机辅助的方法测量一座桥的长度．如图，桥 $\mathit{AB}$是水平并且笔直的，测量过程中，小组成员遥控无人机飞到桥 $\mathit{AB}$的上方120米的点 $C$处悬停，此时测得桥两端 $A$， $B$两点的俯角分别为 $60°$和 $45°$，求桥 $\mathit{AB}$的长度．