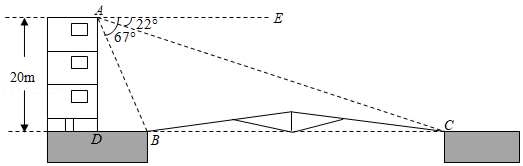
政府将要在某学校大楼前修一座大桥．如图，宋老师测得大楼的高是_优题课试题网

首页 / 初中数学 / 试题详细

更新 2022-09-04
科目数学
题型解答题
难度中等
浏览 237

政府将要在某学校大楼前修一座大桥．如图，宋老师测得大楼的高是20米，大楼的底部 $D$ 处与将要修的大桥 $BC$ 位于同一水平线上，宋老师又上到楼顶 $A$ 处测得 $B$ 和 $C$ 的俯角 $∠ EAB$ ， $∠ EAC$ 分别为 $67 °$ 和 $22 °$ ，宋老师说现在我能算出将要修的大桥 $BC$ 的长了．同学们：你知道宋老师是怎么算的吗？请写出计算过程（结果精确到0.1米）．

其中 $\sin 67 ° \approx \frac{12}{13}$ ， $\cos 67 ° \approx \frac{5}{13}$ ， $\tan 67 ° \approx \frac{12}{5}$ ， $\sin 22 ° \approx \frac{3}{8}$ ， $\cos 22 ° \approx \frac{15}{16}$ ， $\tan 22 ° \approx \frac{2}{5}$

登录免费查看答案和解析

相关试题

某超市拟于中秋节前50天里销售某品牌月饼，其进价为18元 $/ kg$ ．设第 $x$ 天的销售价格为 $y$ （元 $/ kg)$ ，销售量为 $m (kg)$ ．该超市根据以往的销售经验得出以下的销售规律：①当 $1 ⩽ x ⩽ 30$ 时， $y = 40$ ；当 $31 ⩽ x ⩽ 50$ 时， $y$ 与 $x$ 满足一次函数关系，且当 $x = 36$ 时， $y = 37$ ； $x = 44$ 时， $y = 33$ ．② $m$ 与 $x$ 的关系为 $m = 5 x + 50$ ．

（1）当 $31 ⩽ x ⩽ 50$ 时， $y$ 与 $x$ 的关系式为　 $y = - \frac{1}{2} x + 55$ 　；

（2） $x$ 为多少时，当天的销售利润 $W$ （元 $)$ 最大？最大利润为多少？

（3）若超市希望第31天到第35天的日销售利润 $W$ （元 $)$ 随 $x$ 的增大而增大，则需要在当天销售价格的基础上涨 $a$ 元 $/ kg$ ，求 $a$ 的取值范围．

题型：未知
难度：未知

收藏答案/解析

如图， $ΔABC$ 中， $AB = AC$ ，以 $AC$ 为直径的 $⊙ O$ 交 $BC$ 于点 $D$ ，点 $E$ 为 $AC$ 延长线上一点，且 $∠ CDE = \frac{1}{2} ∠ BAC$ ．

（1）求证： $DE$ 是 $⊙ O$ 的切线；

（2）若 $AB = 3 BD$ ， $CE = 2$ ，求 $⊙ O$ 的半径．

题型：未知
难度：未知

收藏答案/解析

已知关于 $x$ 的一元二次方程 $x^{2} - 6 x + 2 a + 5 = 0$ 有两个不相等的实数根 $x_{1}$ ， $x_{2}$ ．

（1）求 $a$ 的取值范围；

（2）若 $x_{1}^{2} + x_{2}^{2} - x_{1} x_{2} ⩽ 30$ ，且 $a$ 为整数，求 $a$ 的值．

题型：未知
难度：未知

收藏答案/解析

第一盒中有2个白球、1个黄球，第二盒中有1个白球、1个黄球，这些球除颜色外无其他差别．

（1）若从第一盒中随机取出1个球，则取出的球是白球的概率是　　．

（2）若分别从每个盒中随机取出1个球，请用列表或画树状图的方法求取出的两个球中恰好1个白球、1个黄球的概率．

题型：未知
难度：未知

收藏答案/解析

如图，拦水坝的横断面为梯形 $ABCD$ ， $AD = 3 m$ ，坝高 $AE = DF = 6 m$ ，坡角 $α = 45 °$ ， $β = 30 °$ ，求 $BC$ 的长．

题型：未知
难度：未知

收藏答案/解析

相关知识点

解直角三角形的应用-仰角俯角问题

推荐套卷

热门套卷

粤ICP备20024846号

粤公网安备

粤公网安备 44130202000953号

Copyright ©2020-2025 优题课 youtike.com 版权所有 Powered by：Youtike Platform 6.8.8

声明：本网站部分内容由互联网用户自发贡献自行上传，本网站不拥有所有权，也不承担相关法律责任。
如果您发现有涉嫌版权的内容，欢迎发送邮件至：service@youtike.com 或联系QQ：267757 进行举报，一经查实，本站将立刻删除涉嫌侵权内容。