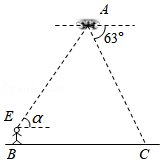
随着科学技术的不断进步，无人机被广泛应用到实际生活中，小星利

更新 2022-09-04
科目数学
题型解答题
难度未知
浏览 227

随着科学技术的不断进步，无人机被广泛应用到实际生活中，小星利用无人机来测量广场 $B$ ， $C$ 两点之间的距离．如图所示，小星站在广场的 $B$ 处遥控无人机，无人机在 $A$ 处距离地面的飞行高度是 $41.6 m$ ，此时从无人机测得广场 $C$ 处的俯角为 $63 °$ ，他抬头仰视无人机时，仰角为 $α$ ，若小星的身高 $BE = 1.6 m$ ， $EA = 50 m$ （点 $A$ ， $E$ ， $B$ ， $C$ 在同一平面内）．

（1）求仰角 $α$ 的正弦值；

（2）求 $B$ ， $C$ 两点之间的距离（结果精确到 $1 m)$ ．

$(\sin 63 ° \approx 0.89$ ， $\cos 63 ° \approx 0.45$ ， $\tan 63 ° \approx 1.96$ ， $\sin 27 ° \approx 0.45$ ， $\cos 27 ° \approx 0.89$ ， $\tan 27 ° \approx 0.51)$

登录免费查看答案和解析

相关试题

为积极响应“弘扬传统文化”的号召，某学校倡导全校1200名学生进行经典诗词诵背活动，并在活动之后举办经典诗词大赛，为了解本次系列活动的持续效果，学校团委在活动启动之初，随机抽取部分学生调查“一周诗词诵背数量”，根据调查结果绘制成的统计图（部分）如图所示．

大赛结束后一个月，再次抽查这部分学生“一周诗词诵背数量”，绘制成统计表

一周诗词诵背数量	3首	4首	5首	6首	7首	8首
人数	10	10	15	40	25	20

请根据调查的信息分析：

（1）活动启动之初学生“一周诗词诵背数量”的中位数为　　；

（2）估计大赛后一个月该校学生一周诗词诵背6首（含6首）以上的人数；

（3）选择适当的统计量，从两个不同的角度分析两次调查的相关数据，评价该校经典诗词诵背系列活动的效果．

题型：未知
难度：未知

收藏答案/解析

如图，将矩形 $ABCD$ （纸片）折叠，使点 $B$ 与 $AD$ 边上的点 $K$ 重合， $EG$ 为折痕；点 $C$ 与 $AD$ 边上的点 $K$ 重合， $FH$ 为折痕．已知 $∠ 1 = 67.5 °$ ， $∠ 2 = 75 °$ ， $EF = \sqrt{3} + 1$ ，求 $BC$ 的长．

题型：未知
难度：未知

收藏答案/解析

某自动化车间计划生产480个零件，当生产任务完成一半时，停止生产进行自动化程序软件升级，用时20分钟，恢复生产后工作效率比原来提高了 $\frac{1}{3}$ ，结果完成任务时比原计划提前了40分钟，求软件升级后每小时生产多少个零件？

题型：未知
难度：未知

收藏答案/解析

我国古代数学著作《九章算术》中有这样一题，原文是：“今有大器五小器一容三斛，大器一小器五容二斛，问大小器各容几何．”意思是：有大小两种盛酒的桶，已知5个大桶加上1个小桶可以盛酒3斛（斛，是古代的一种容量单位），1个大桶加上5个小桶可以盛酒2斛．1个大桶、1个小桶分别可以盛酒多少斛？请解答．

题型：未知
难度：未知

收藏答案/解析

如图，在平面直角坐标系中，抛物线 $y = a x^{2} + bx + c (a \neq 0)$ 与 $x$ 轴交于 $A$ 、 $B$ 两点，与 $y$ 轴交于点 $C$ ，且 $OA = 2$ ， $OB = 8$ ， $OC = 6$ ．

（1）求抛物线的解析式；

（2）点 $M$ 从 $A$ 点出发，在线段 $AB$ 上以每秒3个单位长度的速度向 $B$ 点运动，同时，点 $N$ 从 $B$ 出发，在线段 $BC$ 上以每秒1个单位长度的速度向 $C$ 点运动，当其中一个点到达终点时，另一个点也停止运动，当 $ΔMBN$ 存在时，求运动多少秒使 $ΔMBN$ 的面积最大，最大面积是多少？

（3）在（2）的条件下， $ΔMBN$ 面积最大时，在 $BC$ 上方的抛物线上是否存在点 $P$ ，使 $ΔBPC$ 的面积是 $ΔMBN$ 面积的9倍？若存在，求点 $P$ 的坐标；若不存在，请说明理由．

题型：未知
难度：未知

收藏答案/解析