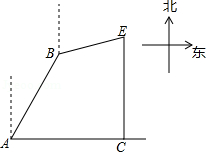
如图,海岛 在海岛 的北偏东30方向,且与海岛 相距20海里,一艘渔船从海岛 出发,以5海里 时的速度沿北偏东 方向航行,同时一艘快艇从海岛 出发,向正东方向航行.2小时后,快艇到达 处,此时渔船恰好到达快艇正北方向的 处.
(1)求 的度数;
(2)求快艇的速度及 , 之间的距离.
(参考数据: , , ,
相关知识点
推荐套卷
如图,海岛 在海岛 的北偏东30方向,且与海岛 相距20海里,一艘渔船从海岛 出发,以5海里 时的速度沿北偏东 方向航行,同时一艘快艇从海岛 出发,向正东方向航行.2小时后,快艇到达 处,此时渔船恰好到达快艇正北方向的 处.
(1)求 的度数;
(2)求快艇的速度及 , 之间的距离.
(参考数据: , , ,
