从“中国环境保护部数据中心”获得某市环保监测站提供的资料,从中随机抽取
了今年1~3月份中的30天的空气污染指数(API)如下:
64, 100, 61, 60, 59, 108, 78, 63, 101, 63, 69, 69, 104, 72, 45, 54, 75, 57, 78, 87, 124, 115, 98, 87, 78, 86, 106, 70, 79, 73.
空气质量级别表
空气污染
指数
|
0~50
|
51~100
|
101~150
|
151~200
|
201~250
|
251~300
|
300以上
|
空气质量
级别
|
I级
|
Ⅱ级
|
Ⅲ(1)级
|
Ⅲ(2)级
|
Ⅳ(1)级
|
Ⅳ(1)级
|
Ⅴ级
|
空气质量
状况
|
优
|
良
|
轻微污染
|
轻度污染
|
中度污染
|
中度重
污染
|
重度
污染
|
请你根据空气质量级别表和上述空气污染指数,解答以下问题:
(1)填写频率分布表中未完成的空格;
分组
|
频数统计
|
频数
|
频率
|
0~50
|
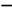
|
1
|
0.03
|
51~100
|
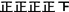
|
23
|
①
|
101~150
|
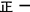
|
6
|
②
|
合计
|
30
|
30
|
1.00
|
(2)写出统计数据中的中位数、众数;
(3)利用以上信息,试估计该市今年(按360天计算)空气质量是优良(包括Ⅰ、Ⅱ级)的天数.