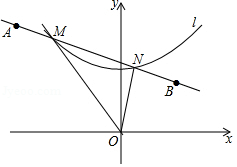
如图,曲线 是由函数 在第一象限内的图象绕坐标原点 逆时针旋转 得到的,过点 , , , 的直线与曲线 相交于点 、 ,则 的面积为 .
如图,矩形 的顶点 在坐标原点,顶点 , 分别在 , 轴的正半轴上,顶点 在反比例函数 为常数, , 的图象上,将矩形 绕点 按逆时针方向旋转 得到矩形 ,若点 的对应点 恰好落在此反比例函数图象上,则 的值是 .

如图,在平面直角坐标系中,将 沿 轴向右滚动到△ 的位置,再到△ 的位置 依次进行下去,若已知点 , ,则点 的坐标为

A. B. C. D.
如图,在平面直角坐标系中,将正方形 绕点 逆时针旋转 后得到正方形 ,依此方式,绕点 连续旋转2018次得到正方形 ,如果点 的坐标为 ,那么点 的坐标为

A. B. C. D.
如图,在平面直角坐标系中,已知点 ,以点 为旋转中心,将点 逆时针旋转到点 的位置,则 的长为 .

如图,矩形 的边 在 轴上,点 在第二象限,点 在第一象限, , ,将矩形 绕点 旋转,使点 落在 轴上,则点 对应点的坐标是

A. , B.
C. 或 D. , 或
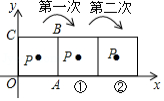
如图,把正方形铁片 置于平面直角坐标系中,顶点 的坐标为 ,点 在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转 ,第一次旋转至图①位置,第二次旋转至图②位置 ,则正方形铁片连续旋转2017次后,点 的坐标为 .
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为 、 、 (正方形网格中每个小正方形的边长是1个单位长度).
(1)△A1B1C1是△ABC绕点 逆时针旋转 度得到的,B1的坐标是 ;
(2)求出线段AC旋转过程中所扫过的面积(结果保留π).

如图,△ABC三个顶点的坐标分别为A(﹣1,3),B(﹣4,1),C(﹣2,1).
(1)请画出△ABC向右平移5个单位长度后得到的△A1B1C1.
(2)请画出△A1B1C1关于原点对称的△A2B2C2.
(3)求四边形ABA2B2的面积.

如图,在平面直角坐标系中, , , .先将四边形ABCD沿x轴翻折,再向右平移8个单位长度,向下平移1个单位长度后,得到四边形A1B1C1D1,最后将四边形A1B1C1D1,绕着点A1旋转,使旋转后的四边形对角线的交点落在x轴上,则旋转后的四边形对角线的交点坐标为( )

A.(4,0)B.(5,0)
C.(4,0)或(﹣4,0)D.(5,0)或(﹣5,0)
如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ ABC的三个顶点的坐标分别为 A(﹣1,3), B(﹣4,0), C(0,0)
(1)画出将△ ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△ A 1 B 1 C 1;
(2)画出将△ ABC绕原点 O顺时针方向旋转90°得到△ A 2 B 2 O;
(3)在 x轴上存在一点 P,满足点 P到 A 1与点 A 2距离之和最小,请直接写出 P点的坐标.
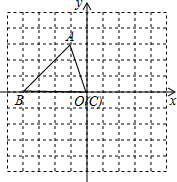
将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若 ,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( )

A. B. C. D.
在平面直角坐标系中,点 A的坐标为(1, ),以原点 O为中心,将点 A顺时针旋转60°得到点 A',则点 A′的坐标为( )
| A. |
(0, ) |
B. |
(1,﹣ ) |
C. |
(﹣1, ) |
D. |
(2,0) |
如图,正三角形 ABO的边长为2, O为坐标原点,点 A在 x轴上,点 B在第二象限,△ ABO沿 x轴正方向做无滑动的翻滚,经一次翻滚后得△ A 1 B 1 O,则翻滚三次后点 B的对应点的坐标是 ,翻滚90次后 AB的中点 M经过的路径长为 .
