如图,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 ,连接 ,若将 绕点 顺时针旋转 ,得到△ ,则点 的坐标为 .

如图,在平面直角坐标系中,已知 , , ,将 先向右平移3个单位长度得到△ ,再绕 顺时针方向旋转 得到△ ,则 的坐标是 .

如图,在平面直角坐标系中, 斜边上的高为1, ,将 绕原点顺时针旋转 得到 ,点 的对应点 恰好在函数 的图象上,若在 的图象上另有一点 使得 ,则点 的坐标为 .

如图,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 ,将点 绕点 顺时针旋转 得到点 ,则点 的坐标为 .

如图,已知点 , , , ,连接 , ,将线段 绕着某一点旋转一定角度,使其与线段 重合(点 与点 重合,点 与点 重合),则这个旋转中心的坐标为 .

如图,将正方形网格放置在平面直角坐标系中,其中,每个小正方形的边长均为1,点 , , 的坐标分别为 , , .△ 是 关于 轴的对称图形,将△ 绕点 逆时针旋转 ,点 的对应点为 ,则点 的坐标为 .

如图,直线 与 轴、 轴分别交于 、 两点,把 绕点 逆时针旋转 后得到△ ,则点 的坐标是 .

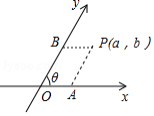
如图,把平面内一条数轴 绕原点 逆时针旋转角 得到另一条数轴 , 轴和 轴构成一个平面斜坐标系.规定:过点 作 轴的平行线,交 轴于点 ,过点 作 轴的平行线,交 轴于点 ,若点 在 轴上对应的实数为 ,点 在 轴上对应的实数为 ,则称有序实数对 为点 的斜坐标,在某平面斜坐标系中,已知 ,点 的斜坐标为 ,点 与点 关于 轴对称,则点 的斜坐标为 .
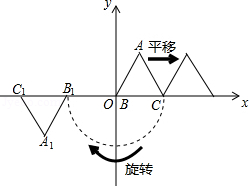
定义:在平面直角坐标系中,一个图形先向右平移 个单位,再绕原点按顺时针方向旋转 角度,这样的图形运动叫作图形的 变换.
如图,等边 的边长为1,点 在第一象限,点 与原点 重合,点 在 轴的正半轴上.△ 就是 经 变换后所得的图形.
若 经 变换后得△ ,△ 经 变换后得△ ,△ 经 变换后得△ ,依此类推
△ 经 变换后得△ ,则点 的坐标是 ,点 的坐标是 .
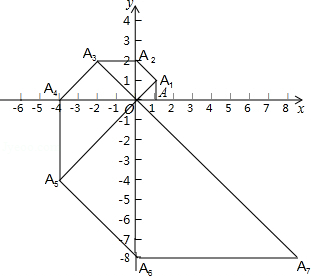
如图,在平面直角坐标系中,等腰直角三角形 的直角边 在 轴上,点 在第一象限,且 ,以点 为直角顶点, 为一直角边作等腰直角三角形 ,再以点 为直角顶点, 为直角边作等腰直角三角形 依此规律,则点 的坐标是 .
在平面直角坐标系中的位置如图所示, ,将 绕 点,逆时针旋转 得到△ , ,交 轴于 ,若△ △ ,则点 的坐标 .

如图,平面直角坐标系中,矩形 的顶点 , , .将矩形 绕点 顺时针方向旋转,使点 恰好落在 上的点 处,则点 的对应点 的坐标为 .

如图,在平面直角坐标系 中,菱形 的边长为2,点 在第一象限,点 在 轴正半轴上, ,若将菱形 绕点 顺时针旋转 ,得到四边形 ,则点 的对应点 的坐标为 .
