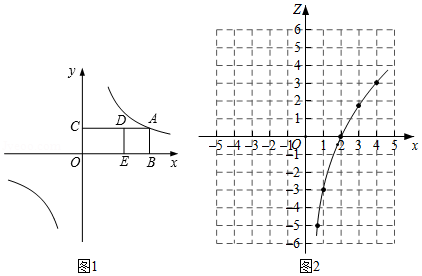
图1是邻边长为2和6的矩形,它由三个小正方形组成,将其剪拼成不重叠、无缝隙的大正方形(如图 ,则图1中所标注的 的值为 ;记图1中小正方形的中心为点 , , ,图2中的对应点为点 , , .以大正方形的中心 为圆心作圆,则当点 , , 在圆内或圆上时,圆的最小面积为 .
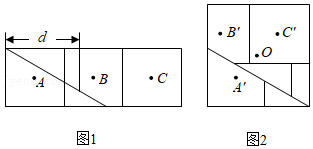
电子体重秤读数直观又便于携带,为人们带来了方便.某综合实践活动小组设计了简易电子体重秤:制作一个装有踏板(踏板质量忽略不计)的可变电阻 , 与踏板上人的质量 之间的函数关系式为 (其中 , 为常数, ,其图象如图1所示;图2的电路中,电源电压恒为8伏,定值电阻 的阻值为30欧,接通开关,人站上踏板,电压表显示的读数为 ,该读数可以换算为人的质量 ,
温馨提示:①导体两端的电压 ,导体的电阻 ,通过导体的电流 ,满足关系式 ;
②串联电路中电流处处相等,各电阻两端的电压之和等于总电压

(1)求 , 的值;
(2)求 关于 的函数解析式;
(3)用含 的代数式表示 ;
(4)若电压表量程为 伏,为保护电压表,请确定该电子体重秤可称的最大质量.
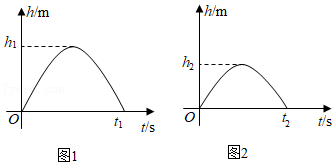
以初速度 (单位: 从地面竖直向上抛出小球,从抛出到落地的过程中,小球的高度 (单位: 与小球的运动时间 (单位: 之间的关系式是 .现将某弹性小球从地面竖直向上抛出,初速度为 ,经过时间 落回地面,运动过程中小球的最大高度为 (如图 ;小球落地后,竖直向上弹起,初速度为 ,经过时间 落回地面,运动过程中小球的最大高度为 (如图 .若 ,则 .
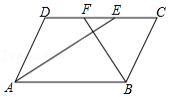
问题:如图,在 中, , , , 的平分线 , 分别与直线 交于点 , ,求 的长.
答案: .
探究:(1)把"问题"中的条件" "去掉,其余条件不变.
①当点 与点 重合时,求 的长;
②当点 与点 重合时,求 的长.
(2)把"问题"中的条件" , "去掉,其余条件不变,当点 , , , 相邻两点间的距离相等时,求 的值.
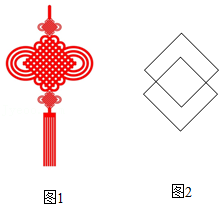
数学兴趣小组同学从"中国结"的图案(图 中发现,用相同的菱形纵向排列放置,可得到更多的菱形.如图2,用2个相同的菱形放置,得到3个菱形.下面说法正确的是
| A. |
用3个相同的菱形放置,最多能得到6个菱形 |
| B. |
用4个相同的菱形放置,最多能得到16个菱形 |
| C. |
用5个相同的菱形放置,最多能得到27个菱形 |
| D. |
用6个相同的菱形放置,最多能得到41个菱形 |
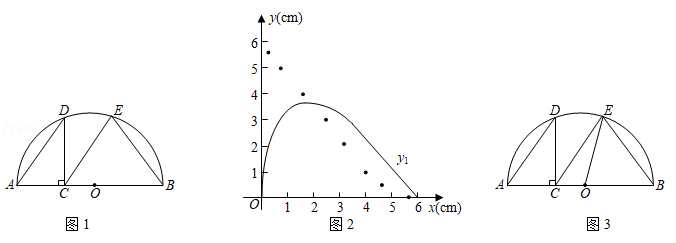
如图1,点 是半圆 的直径 上一动点(不包括端点), ,过点 作 交半圆于点 ,连结 ,过点 作 交半圆于点 ,连结 .牛牛想探究在点 运动过程中 与 的大小关系.他根据学习函数的经验,记 , , .请你一起参与探究函数 、 随自变量 变化的规律.
通过几何画板取点、画图、测量,得出如下几组对应值,并在图2中描出了以各对对应值为坐标的点,画出了不完整图象.
|
|
|
0.30 |
0.80 |
1.60 |
2.40 |
3.20 |
4.00 |
4.80 |
5.60 |
|
|
|
|
2.01 |
2.98 |
3.46 |
3.33 |
2.83 |
2.11 |
1.27 |
0.38 |
|
|
|
|
5.60 |
4.95 |
3.95 |
2.96 |
2.06 |
1.24 |
0.57 |
0.10 |
|
(1)当 时, .
(2)在图2中画出函数 的图象,并结合图象判断函数值 与 的大小关系.
(3)由(2)知" 取某值时,有 ".如图3,牛牛连结了 ,尝试通过计算 , 的长来验证这一结论,请你完成计算过程.
如图1是一座抛物线型拱桥侧面示意图.水面宽 与桥长 均为 ,在距离 点6米的 处,测得桥面到桥拱的距离 为 ,以桥拱顶点 为原点,桥面为 轴建立平面直角坐标系.
(1)求桥拱顶部 离水面的距离.
(2)如图2,桥面上方有3根高度均为 的支柱 , , ,过相邻两根支柱顶端的钢缆呈形状相同的抛物线,其最低点到桥面距离为 .
①求出其中一条钢缆抛物线的函数表达式.
②为庆祝节日,在钢缆和桥拱之间竖直装饰若干条彩带,求彩带长度的最小值.
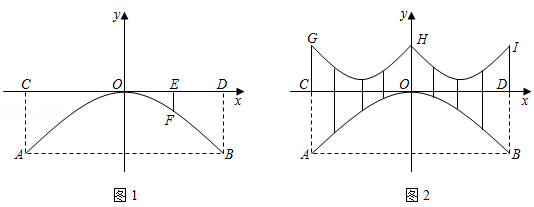
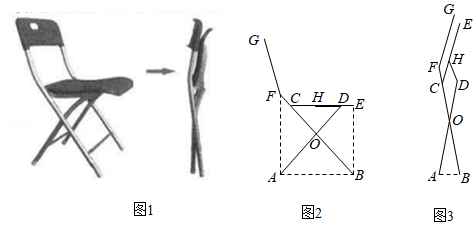
图1是某折叠式靠背椅实物图,图2是椅子打开时的侧面示意图,椅面 与地面平行,支撑杆 , 可绕连接点 转动,且 ,椅面底部有一根可以绕点 转动的连杆 ,点 是 的中点, , 均与地面垂直,测得 , , .
(1)椅面 的长度为 .
(2)如图3,椅子折叠时,连杆 绕着支点 带动支撑杆 , 转动合拢,椅面和连杆夹角 的度数达到最小值 时, , 两点间的距离为 (结果精确到 .
(参考数据: , ,
【证明体验】
(1)如图1, 为 的角平分线, ,点 在 上, .求证: 平分 .
【思考探究】
(2)如图2,在(1)的条件下, 为 上一点,连结 交 于点 .若 , , ,求 的长.
【拓展延伸】
(3)如图3,在四边形 中,对角线 平分 , ,点 在 上, .若 , , ,求 的长.

如图,在矩形 中,点 在边 上, 与 关于直线 对称,点 的对称点 在边 上, 为 中点,连结 分别与 , 交于 , 两点.若 , ,则 的长为 , 的值为 .

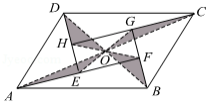
如图是一个由5张纸片拼成的平行四边形 ,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为 ,另两张直角三角形纸片的面积都为 ,中间一张矩形纸片 的面积为 , 与 相交于点 .当 , , , 的面积相等时,下列结论一定成立的是
| A. |
|
B. |
|
C. |
|
D. |
|
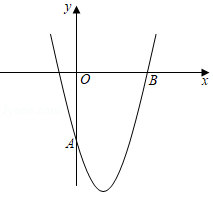
如图,已知抛物线 经过点 , .
(1)求 , 的值;
(2)连结 ,交抛物线 的对称轴于点 .
①求点 的坐标;
②将抛物线 向左平移 个单位得到抛物线 .过点 作 轴,交抛物线 于点 . 是抛物线 上一点,横坐标为 ,过点 作 轴,交抛物线 于点 ,点 在抛物线 对称轴的右侧.若 ,求 的值.
背景:点 在反比例函数 的图象上, 轴于点 , 轴于点 ,分别在射线 , 上取点 , ,使得四边形 为正方形.如图1,点 在第一象限内,当 时,小李测得 .
探究:通过改变点 的位置,小李发现点 , 的横坐标之间存在函数关系.请帮助小李解决下列问题.
(1)求 的值.
(2)设点 , 的横坐标分别为 , ,将 关于 的函数称为" 函数".如图2,小李画出了 时" 函数"的图象.
①求这个" 函数"的表达式.
②补画 时" 函数"的图象,并写出这个函数的性质(两条即可).
③过点 作一直线,与这个" 函数"图象仅有一个交点,求该交点的横坐标.