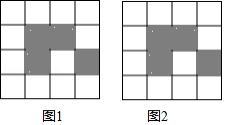
如图,下列 网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.
(1)在图1中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形;
(2)在图2中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
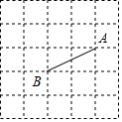
如图,在 的正方形网格中有一条线段 ,点 与点 均在格点上.请在这个网格中作线段 的垂直平分线.要求:①仅用无刻度直尺,且不能用直尺中的直角;②保留必要的作图痕迹.
如图, 是 的角平分线.
(1)作线段 的垂直平分线 ,分别交 、 于点 、 ;(用直尺和圆规作图,标明字母,保留作图痕迹,不写作法.
(2)连接 、 ,四边形 是 形.(直接写出答案)

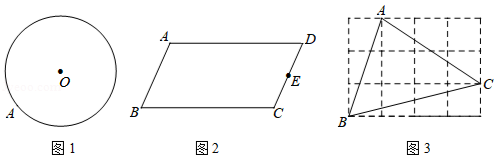
按要求作图,不要求写作法,但要保留作图痕迹.
(1)如图1, 为 上一点,请用直尺(不带刻度)和圆规作出 的内接正方形;
(2)我们知道,三角形具有性质:三边的垂直平分线相交于同一点,三条角平分线相交于一点,三条中线相交于一点,事实上,三角形还具有性质:三条高所在直线相交于一点.
请运用上述性质,只用直尺(不带刻度)作图.
①如图2,在 中, 为 的中点,作 的中点 .
②如图3,在由小正方形组成的 的网格中, 的顶点都在小正方形的顶点上,作 的高 .
如图, 为半圆 的直径, 为半圆上一点, .
(1)请用直尺(不含刻度)与圆规在 上作一点 ,使得直线 平分 的周长;(不要求写作法,但要保留作图痕迹)
(2)在(1)的条件下,若 , ,求 的面积.

如图, 中, , , .
(1)用直尺和圆规作 的垂直平分线;(保留作图痕迹,不要求写作法)
(2)若(1)中所作的垂直平分线交 于点 ,求 的长.
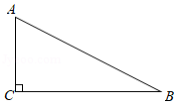
如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中, 的三个顶点 、 、 均在格点上.
(1)画出 关于 轴对称的△ ,并写出点 的坐标;
(2)画出 绕原点 顺时针旋转 后得到的△ ,并写出点 的坐标;
(3)在(2)的条件下,求线段 在旋转过程中扫过的面积(结果保留 .
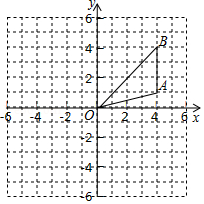
如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中, 的三个顶点 、 、 均在格点上.
(1)画出 关于 轴对称的△ ,并写出点 的坐标;
(2)画出 绕原点 顺时针旋转 后得到的△ ,并写出点 的坐标;
(3)在(2)的条件下,求线段 在旋转过程中扫过的面积(结果保留 .
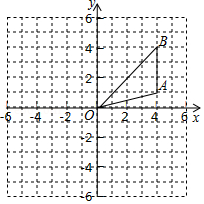
如图,在平面直角坐标系中, 的三个顶点的坐标分别为 , , .(每个小方格都是边长为1个单位长度的正方形)
(1)将 先向上平移2个单位长度,再向右平移4个单位长度得到△ (点 、 、 的对应点分别为点 、 、 ,画出平移后的△ ;
(2)将△ 绕着坐标原点 顺时针旋转 得到△ (点 、 、 的对应点分别为点 、 、 ,画出旋转后的△ ;
(3)求△ 在旋转过程中,点 旋转到点 所经过的路径的长.(结果用含 的式子表示)
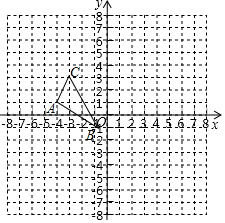
如图,在正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内, 的三个顶点坐标分别为 , , .
(1)画出 关于 轴对称的△ .
(2)画出 绕点 逆时针旋转 后得到的△ .
(3)在(2)的条件下,求点 所经过的路径长(结果保留 .
如图,方格纸中每个小正方形的边长均为1,线段 的两个端点均在小正方形的顶点上.
(1)在图中画出以线段 为一边的矩形 (不是正方形),且点 和点 均在小正方形的顶点上;
(2)在图中画出以线段 为一腰,底边长为 的等腰三角形 ,点 在小正方形的顶点上,连接 ,请直接写出线段 的长.

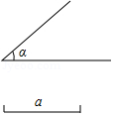
尺规作图(只保留作图痕迹,不要求写出作法).
如图,已知 和线段 ,求作 ,使 , , .
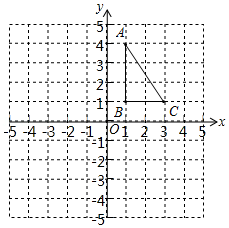
如图, 三个顶点的坐标分别为 , ,
(1)请画出将 向左平移4个单位长度后得到的图形△ ;
(2)请画出 关于原点 成中心对称的图形△ ;
(3)在 轴上找一点 ,使 的值最小,请直接写出点 的坐标.