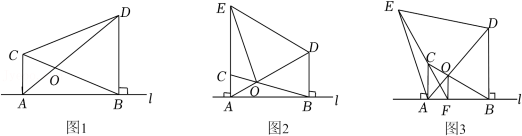
已知:点 均在直线 的上方, 与 都是直线 的垂线段,且 在 的右侧, , 与 相交于点 .
(1)如图1,若连接 ,则 的形状为 , 的值为 ;
(2)若将 沿直线 平移,并以 为一边在直线 的上方作等边 .
①如图2,当 与 重合时,连接 ,若 ,求 的长;
②如图3,当 时,连接 并延长交直线 于点 ,连接 .求证: .
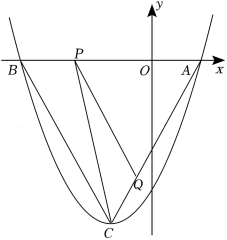
如图,已知抛物线 经过 和 两点,直线 与 轴相交于点 , 是直线 上方的抛物线上的一个动点, 轴交 于点 .
(1)求该抛物线的表达式;
(2)若 轴交 于点 ,求 的最大值;
(3)若以 为顶点的三角形与 相似,请直接写出所有满足条件的点 ,点 的坐标.

如图,在 中, ,点 是 边的中点,点 在 边上, 经过点 且与 边相切于点 , .
(1)求证: 是 的切线;
(2)若 , ,求 的半径及 的长.

综合与实践
“善思”小组开展“探究四点共圆的条件”活动,得出结论:对角互补的四边形四个顶点共圆.该小组继续利用上述结论进行探究.
提出问题:
如图1,在线段AC同侧有两点 ,连接 ,如果 ,那么 四点在同一个圆上.
探究展示:
如图2,作经过点 的 ,在劣弧 上取一点 (不与 重合),连接 ,则 (依据1)
∵
∴
∴点 四点在同一个圆上(对角互补的四边形四个顶点共圆)
∴点 在点 所确定的 上(依据2)
∴点 四点在同一个圆上
反思归纳:
(1)上述探究过程中的“依据1”、“依据2”分别是指什么?
依据1:__________;依据2:__________.
(2)如图3,在四边形 中, ,则 的度数为_____.
拓展探究:
(3)如图4,已知 是等腰三角形, ,点 在 上(不与 的中点重合),连接 .作点 关于 的对称点 ,连接 并延长交 的延长线于 ,连接 .
①求证: 四点共圆;
②若 , 的值是否会发生变化,若不变化,求出其值;若变化,请说明理由.


在平面直角坐标系中,抛物线 (b是常数)经过点(2,0).点A在抛物线上,且点A的横坐标为m(m≠0).以点A为中心,构造正方形PQMN,PQ=2|m|,且PQ⊥x轴.
(1)求该抛物线对应的函数表达式;
(2)若点B是抛物线上一点,且在抛物线对称轴左侧.过点B作x轴的平行线交抛物线于另一点C,连结BC.当BC=4时,求点B的坐标;
(3)若m>0,当抛物线在正方形内部的点的纵坐标y随x的增大而增大时,或者y随x的增大而减小时,求m的取值范围;
(4)当抛物线与正方形PQMN的边只有2个交点,且交点的纵坐标之差为 时,直接写出m的值.
如图,在▱ABCD中, , ,点M为边AB的中点.动点P从点A出发,沿折线 以每秒 个单位长度的速度向终点B运动,连结PM.作点A关于直线PM的对称点 ,连结 、 .设点P的运动时间为t秒,
(1)点D到边AB的距离为 ;
(2)用含t的代数式表示线段DP的长;
(3)连结 ,当线段 最短时,求 的面积;
(4)当 、 、 三点共线时,直接写出t的值.

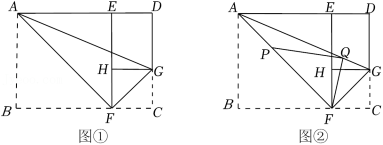
【探索发现】在一次折纸活动中,小亮同学选用了常见的A4纸,如图①,矩形ABCD为它的示意图.他查找了A4纸的相关资料,根据资料显示得出图①中 .他先将A4纸沿过点A的直线折叠,使点B落在AD上,点B的对应点为点E,折痕为AF;再沿过点F的直线折叠,使点C落在EF上,点C的对应点为点H,折痕为FG;然后连结AG,沿AG所在的直线再次折叠,发现点D与点F重合,进而猜想 .
【问题解决】小亮对上面△ADG≌△AFG的猜想进行了证明,下面是部分证明过程:
证明:∵四边形ABCD是矩形,
∴ .
由折叠可知, , .
∴ .
∴
请你补全余下的证明过程.
【结论应用】
(1)∠DAG的度数为 度, 的值为 ;
(2)在图①的条件下,点P在线段AF上,且AP AB,点Q在线段AG上,连结FQ、PQ,如图②.设 ,则 的最小值为 .(用含a的代数式表示)
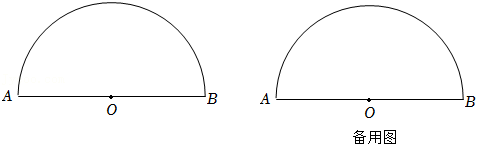
现有若干张相同的半圆形纸片,点O是圆心,直径AB的长是12cm,C是半圆弧上的一点(点C与点A、B不重合),连接AC、BC.
(1)沿AC、BC剪下△ABC,则△ABC是 三角形(填“锐角”、“直角”或“钝角”);
(2)分别取半圆弧上的点E、F和直径AB上的点G、H.已知剪下的由这四个点顺次连接构成的四边形是一个边长为6cm的菱形.请用直尺和圆规在图中作出一个符合条件的菱形(保留作图痕迹,不要求写作法);
(3)经过数次探索,小明猜想,对于半圆弧上的任意一点C,一定存在线段AC上的点M、线段BC上的点N和直径AB上的点P、Q,使得由这四个点顺次连接构成的四边形是一个边长为4cm的菱形.小明的猜想是否正确?请说明理由.
已知二次函数 的自变量x的部分取值和对应函数值y如下表:
|
x |
… |
﹣1 |
0 |
1 |
2 |
3 |
… |
|
y |
… |
4 |
3 |
0 |
﹣5 |
﹣12 |
… |
(1)求二次函数 的表达式;
(2)将二次函数 的图象向右平移k(k>0)个单位,得到二次函数 的图象,使得当﹣1<x<3时,y随x增大而增大;当4<x<5时,y随x增大而减小.请写出一个符合条件的二次函数 的表达式y= ,实数k的取值范围是 ;
(3)A、B、C是二次函数 的图象上互不重合的三点.已知点A、B的横坐标分别是m、m+1,点C与点A关于该函数图象的对称轴对称,求∠ACB的度数.
已知抛物线经过 三点,O为坐标原点,抛物线交正方形 的边 于点 ,点 为射线 上一动点,连接 ,交 于点 .
(1)求抛物线的表达式;
(2)求证: ;
(3)是否存在点 ,使 为等腰三角形?若不存在,请说明理由;若存在,求 的长.

如图,抛物线 ( 是常数)的顶点为 ,与 轴交于 两点, ,点 为线段 上的动点,过 作 交 于点 .
(1)求该抛物线的解析式;
(2)求 面积的最大值,并求此时 点坐标.
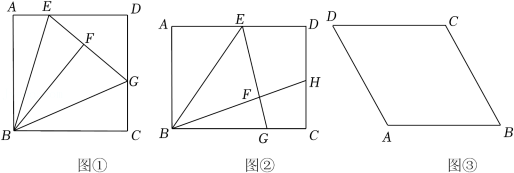
(1)发现:如图①所示,在正方形 中, 为AD边上一点,将 沿 翻折到 处,延长 交 边于 点.求证: ;
(2)探究:如图②,在矩形 中, 为 边上一点,且 .将 沿 翻折到 处,延长 交 边于 点,延长 交 边于点 ,且 ,求 的长.
(3)拓展:如图③,在菱形 中, , 为 边上的三等分点, .将 沿 翻折得到 ,直线 交 于点 ,求 的长.
综合与实践
【问题情境】
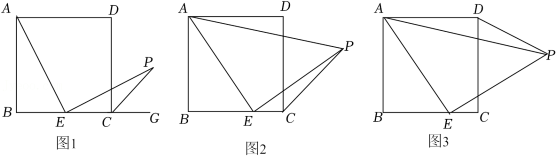
数学活动课上,老师出示了一个问题:如图1,在正方形 中,E是BC的中点, , 与正方形的外角 的平分线交于 点.试猜想 与 的数量关系,并加以证明;
【思考尝试】
(1)同学们发现,取 的中点 ,连接 可以解决这个问题.请在图1中补全图形,解答老师提出的问题.
【实践探究】
(2)希望小组受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形 中, 为 边上一动点(点 不重合), 是等腰直角三角形, ,连接 ,可以求出 的大小,请你思考并解答这个问题.
【拓展迁移】
(3)突击小组深入研究希望小组提出的这个问题,发现并提出新的探究点:如图3,在正方形 中, 为 边上一动点(点 不重合), 是等腰直角三角形, ,连接 .知道正方形的边长时,可以求出 周长的最小值.当 时,请你求出 周长的最小值.
如图,已知抛物线 与 轴交于 两点,与 轴交于点 ,点 为抛物线的顶点.
(1)求抛物线的函数表达式及点 的坐标;
(2)若四边形 为矩形, .点 以每秒 个单位的速度从点 沿 向点 运动,同时点 以每秒 个单位的速度从点 沿 向点 运动,一点到达终点,另一点随之停止.当以 为顶点的三角形与 相似时,求运动时间 的值;
(3)抛物线的对称轴与 轴交于点 ,点 是点 关于点 的对称点,点 是 轴下方抛物线上的动点.若过点 的直线 与抛物线只有一个公共点,且分别与线段 相交于点 ,求证: 为定值.

综合与实践
综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作判断
操作一:对折矩形纸片 ,使 与 重合,得到折痕 ,把纸片展平;
操作二:在 上选一点 ,沿 折叠,使点 落在矩形内部点 处,把纸片展平,连接 .
根据以上操作,当点 在 上时,写出图1中一个 的角:______.
(2)迁移探究
小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片 按照(1)中的方式操作,并延长 交 于点 ,连接 .
①如图2,当点 在 上时, ______ , ______ ;
②改变点 在 上的位置(点 不与点 重合),如图3,判断 与 的数量关系,并说明理由.
(3)拓展应用
在(2)的探究中,已知正方形纸片 的边长为 ,当 时,直接写出 的长.
