在 中, ,点 分别是 , 的中点, 是等腰三角形, ,连接 .
(1)判断线段 和 的关系,并证明你的结论;
(2)连接 ,过点 作 ,过点 作 和 相交于点 ,在图中先补充图形,再判断四边形 的形状,并证明你的结论.

已知,如图,在菱形 中, 为边 的中点, 与对角线 交于点 ,过 作 于点 .

(1)若 ,求 的长;
(2)求证: .
现有一张矩形纸片 (如图)。其中 ,点 是 的中点,将纸片沿直线 折叠,点 落在四边形 内,记为点 ,求线段 的长.

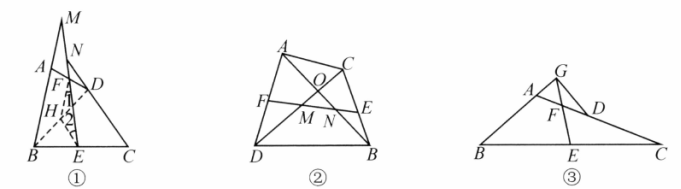
如图①,在四边形 中, 分别是 的中点,连接 并延长,分别与 的延长线交于点 ,则 .
(温馨提示:在图①中,连接 ,取 的中点 ,连接 ,根据三角形中位线定理,证明 ,从而 ,再利用平行线性质,可证 .)
(1)如图②,在四边形 中, 与 相交于点 分别是 的中点,连接 ,分别交 于点 ,判断 的形状,并给予证明;
(2)如图③,在 中, 点在 上, 分别是 的中点,连接 并延长,与 的延长线交于 ,若 ,连接 ,判断 的形状并证明.
几何模型:
条件:如图①, . 是直线 同旁的两个定点
问题:在直线 上确定一点 ,使 的值最小.
方法:作点 关于直线 的对称点 ,连接 交 于点 ,则 的值最小(不必证明).
模型应用:
(1)如图②,正方形 的边长为 , 为 的中点, 是 上一动点.连接 ,由正方形对称性可知, 与 关于直线 对称.连接 交于 于 ,则 的最小值是_____;
(2)如图③, 是 内一点, 分别是 上的动点,求 周长的最小值.

如图所示, 为线段 上一动点,分别过点 作 , ,连接 .已知 ,设 .
(1)用含 的代数式表示 的长;
(2)请问点 满足什么条件时, 的值最小?
(3)根据(2)中的规律和结论,请构图求出代数式 的最小值.

如图,在 中, 分别是 上两点,若 ,试判断 之间的数量关系,并说明理由.

已知 为等腰直角三角形, 为斜边 的中点, 分别是 边上的点,且 .若 .求 的面积.

如图,在 中, 于 ,设 , .

求证:(1) ;
(2) ;
(3)以 为边的三角形是直角三角形.