(本小题13分)如图,四边形 是矩形,点
是矩形,点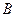 的坐标为
的坐标为 ,直线
,直线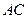 和直线
和直线 相交于点
相交于点 ,点
,点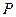 是
是 的中点,
的中点, ,垂足为
,垂足为 .
.
 求直线
求直线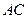 的解析式;
的解析式; 求经过点
求经过点 、
、 、
、 的抛物线的解析式;
的抛物线的解析式; 在抛物线上是否存在
在抛物线上是否存在 ,使得
,使得 ,若存在,求出点
,若存在,求出点 的坐标,若不存在,请说明理由。
的坐标,若不存在,请说明理由。
(本小题8分)如图,下列网格中,每个小方格的边长都是1.
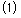 分别作出四边形
分别作出四边形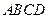 关于
关于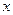 轴、
轴、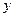 轴、原点的对称图形;
轴、原点的对称图形;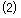 求出四边形
求出四边形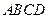 的面积.
的面积.
如图,在平面直角坐标系xoy中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴l与x轴相交于点M.
(1)求抛物线的解析式和对称轴;
(2)设点P为抛物线(x>5)上的一点,若以A、O、M、P为顶点的四边形四条边的长度为四个连续的正整数,请你直接写出点P的坐标;
(3)连接AC.探索:在直线AC下方的抛物线上是否存在一点N,使△NAC的面积最大?若存在,请你求出点N的坐标;若不存在,请你说明理由.
如图,⊙P与y轴相切于坐标原点O(0,0),与x轴相交于点A(5,0),过点A的直线AB与y轴的正半轴交于点B,与⊙P交于点C.
(1)已知AC=3,求点B的坐标;
(2)若AC=a,D是OB的中点.问:点O、P、C、D四点是否在同一圆上?请说明理由.如果这四点在同一圆上,记这个圆的圆心为O1,函数 的图象经过点O1,求k的值(用含a的代数式表示).
的图象经过点O1,求k的值(用含a的代数式表示).
某养鸡场计划购买甲、乙两种小鸡苗共2 000只进行饲养,已知甲种小鸡苗每只2元,乙种小鸡苗每只3元.
(1)若购买这批小鸡苗共用了4 500元,求甲、乙两种小鸡苗各购买了多少只?
(2)若购买这批小鸡苗的钱不超过4 700元,问应选购甲种小鸡苗至少多少只?
(3)相关资料表明:甲、乙两种小鸡苗的成活率分别为94%和99%,若要使这批小鸡苗的成活率不低于96%且买小鸡的总费用最小,问应选购甲、乙两种小鸡苗各多少只?总费用最小是多少元?
。
某学校要印制一批《学生手册》,甲印刷厂提出:每本收1元印刷费,另收500元制版费;乙印刷厂提出:每本收2元印刷费,不收制版费.
(1)分别写出甲、乙两厂的收费y甲(元)、y乙(元)与印制数量x(本)之间的关系式;
(2)问:该学校选择哪间印刷厂印制《学生手册》比较合算?请说明理由.
为了解某品牌电风扇销售量的情况,对某商场5月份该品牌甲、乙、丙三种型号的电风扇销售量进行统计,绘制如下两个统计图(均不完整).请你结合图中的信息,解答下列问题:
(1)该商场5月份售出这种品牌的电风扇共多少台?
(2)若该商场计划订购这三种型号的电风扇共2000台,根据5月份销售量的情况,求该商场应订购丙种型号电风扇多少台比较合理?
从甲学校到乙学校有A1、A2、A3三条线路,从乙学校到丙学校有B1、B2二条线路.
(1)利用树状图或列表的方法表示从甲学校到丙学校的线路中所有可能出现的结果;
(2)小张任意走了一条从甲学校到丙学校的线路,求小张恰好经过了B1线路的概率是多少?
十边形有多少条对角线?若将十边形的对角线全部画出比较麻烦,我们可以通过边数较少的多边形的对角线寻找规律,观察下表:
| 边数 |
3 |
4 |
5 |
6 |
7 |
… |
| 对角线数 |
0 |
2 |
5 |
9 |
14 |
… |
| 对角线增加数 |
0 |
2 |
3 |
4 |
5 |
… |
你发现规律了吗?请总结你发现的规律,并写出十边形对角线的条数.
一辆汽车沿着一条南北向的公路来回行驶,某一天早晨从A地出发,晚上最后到达B地.约定向北为正方向(如:+7.4表示汽车向北行驶7.4千米,-6则表示汽车向南行驶6千米),当天的行驶记录如下(单位:千米):+18.3,-9.5,+7.1,-14,-6.2,+13,-6.8,-8.5.请你根据计算回答以下问题:
(1)B地在A地何方,相距多少千米?
(2)若汽车行驶每千米耗油0.0642升,那么这一天共耗油多少升?(结果保留两位有效数字)
如图,在直角梯形ABCD中,∠D=∠BCD=90°,∠B=60°, AB=6,AD=9,
点E是CD上的一个动点(E不与D重合),过点E作EF∥AC,交AD于点F(当E运
动到C时,EF与AC重合巫台).把△DEF沿EF对折,点D的对应点是点G,设DE=x,
△GEF与梯形ABCD重叠部分的面积为y。
(1) 求CD的长及∠1的度数;
(2) 若点G恰好在BC上,求此时x的值;
(3) 求y与x之间的函数关系式。并求x为何值时,y的值最大?最大值是多少?