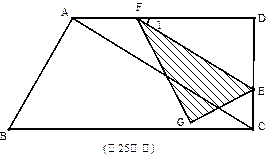如图，在直角梯形ABCD中，∠D∠BCD90°，∠B60°，

首页 / 初中数学 / 试题详细

更新 2022-09-03
科目数学
题型计算题
难度未知
浏览 1054

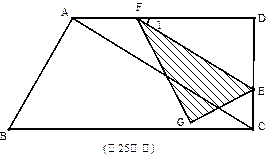
如图，在直角梯形ABCD中，∠D=∠BCD=90°，∠B=60°， AB=6，AD=9，
点E是CD上的一个动点(E不与D重合)，过点E作EF∥AC，交AD于点F(当E运
动到C时，EF与AC重合巫台)．把△DEF沿EF对折，点D的对应点是点G，设DE=x，
△GEF与梯形ABCD重叠部分的面积为y。
(1) 求CD的长及∠1的度数；
(2) 若点G恰好在BC上，求此时x的值；
(3) 求y与x之间的函数关系式。并求x为何值时，y的值最大?最大值是多少?

登录免费查看答案和解析

相关试题

计算： $- 1^{2018} + {(\frac{1}{2})}^{- 2} - | \sqrt{3} - 2 | - 2 \sin 60 °$ ．

题型：未知
难度：未知

收藏答案/解析

（1）计算： $| 2 - \sqrt{3} | + {(\sqrt{2} + 1)}^{0} - 3 \tan 30 ° + {(- 1)}^{2018} - {(\frac{1}{2})}^{- 1}$ ；

（2）解不等式组： $\{\begin{matrix} x + 3 > 0 \\ 2 (x - 1) + 3 ⩾ 3 x . \end{matrix}$ 并判断 $- 1$ ， $\sqrt{2}$ 这两个数是否为该不等式组的解．

题型：未知
难度：未知

收藏答案/解析

先化简，再求值 $\frac{x - 3}{x^{2} - 1} \div \frac{x - 3}{x^{2} + 2 x + 1} - (\frac{1}{x - 1} + 1)$ ，其中 $x$ 是不等式组 $\{\begin{matrix} 5 x - 3 > 3 (x + 1) \\ \frac{1}{2} x - 1 < 9 - \frac{3}{2} x \end{matrix}$ 的整数解．

题型：未知
难度：未知

收藏答案/解析

先化简，再求值： $(x y^{2} + x^{2} y) \times \frac{x}{x^{2} + 2 xy + y^{2}} \div \frac{x^{2} y}{x^{2} - y^{2}}$ ，其中 $x = π^{0} - {(\frac{1}{2})}^{- 1}$ ， $y = 2 \sin 45 ° - \sqrt{8}$ ．

题型：未知
难度：未知

收藏答案/解析

解不等式： $\frac{x - 2}{2} ⩽ \frac{7 - x}{3}$ ．

题型：未知
难度：未知

收藏答案/解析

推荐套卷

热门套卷

粤ICP备20024846号

粤公网安备 44130202000953号

声明：本网站部分内容由互联网用户自发贡献自行上传，本网站不拥有所有权，也不承担相关法律责任。
如果您发现有涉嫌版权的内容，欢迎发送邮件至：service@youtike.com 或联系QQ：267757 进行举报，一经查实，本站将立刻删除涉嫌侵权内容。