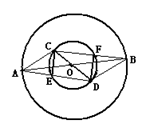
如图,同心⊙O,大⊙O的直径AB=2 ,小⊙O的直径CD=2,连接AC、AD、BD、BC,AD、CB分别交小⊙O于E、F.
,小⊙O的直径CD=2,连接AC、AD、BD、BC,AD、CB分别交小⊙O于E、F.问四边形CEDF是何种特殊四边形?请证明你的结论;
当AC与小⊙O相切时,四边形CEDF是正方形吗?请说明理由.
如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE.求证:AC=AE;
求△ACD外接圆的直径.

如图,⊙O的半径OA⊥弦BC,且∠AOB=60°,D是⊙O上另一点,AD与BC相交于点E,若DC=DE,则正确结论的序号是 (多填或错填得0分,少填酌情给分).
① ; ②
; ② ; ③
; ③ ; ④△AEC∽△ACD.
; ④△AEC∽△ACD.
如图,已知⊙O的半径为2cm,点C是直径AB的延长线上一点,且 ,过点C作⊙O的切线,切点为D,则CD= ★ cm.
,过点C作⊙O的切线,切点为D,则CD= ★ cm.
如图, ⊙O的半径为4㎝, 是⊙O的直径,
是⊙O的直径, 切⊙O于点
切⊙O于点 ,且
,且 =4㎝,当点P在⊙O上运动时,是否存在点P,使得△
=4㎝,当点P在⊙O上运动时,是否存在点P,使得△ 为等腰三角形,若存在,有几个符合条件的点
为等腰三角形,若存在,有几个符合条件的点 ,并分别求出点
,并分别求出点 到线段
到线段 的距离;若不存在,请说明理由.
的距离;若不存在,请说明理由.
已知扇形的圆心角为 ,半径为1,将它沿着箭头方向无滑动滚动到
,半径为1,将它沿着箭头方向无滑动滚动到 位置,
位置,
①点 到
到 的路径是
的路径是



 ;
;
②点 到
到 的路径是
的路径是 ;
;
③点 在
在

 段上运动路线是线段
段上运动路线是线段 ;
;
④点 到
到 的所经过的路径长为
的所经过的路径长为
以上命题正确的是 .
一个边长为4㎝的等边三角形 与⊙
与⊙ 等高,如图放置, ⊙
等高,如图放置, ⊙ 与
与 相切于点
相切于点 ,⊙
,⊙ 与
与 相交于点
相交于点 ,则
,则 的长为 ㎝.
的长为 ㎝.
如图,已知⊙ 是以数轴的原点
是以数轴的原点 为圆心,半径为1的圆,
为圆心,半径为1的圆, ,点
,点 (P与O不重合)在数轴上运动,若过点
(P与O不重合)在数轴上运动,若过点 且与
且与 平行的直线与⊙
平行的直线与⊙ 有公共点, 设点P所表示的实数为
有公共点, 设点P所表示的实数为 ,则
,则 的取值范围是( )
的取值范围是( )
A.  |
B. |
C. |
D. |

如图,AB是半圆O上的直径,E是的中点,OE交弦BC于点D,过点C作⊙O切线交OE的延长线于点F. 已知BC=8,DE=2.求⊙O的半径;
求CF的长;
求tan∠BAD 的值

如图,MN=3,以MN为直径的⊙O1,与一个半径为5的⊙O2相切于点M,正方形ABCD的顶点A,B在大圆上,小圆在正方形的外部且与CD切于点N,则正方形ABCD的边长为 ▲ .
(本题10分)如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.
试判断直线BD与⊙O的位置关系,并证明你的结论.
若⊙O半径为3,OP=1,⊙P与⊙O相切,则⊙P的半径为 ____.
如图,∠A是⊙O的圆周角,∠A=40°,则∠BOC的度数为__________ .第15题图
.第15题图
一条排水管的截面如右图所示,截面中有水部分弓形的弦AB为 cm, 弓形的高为6cm.
cm, 弓形的高为6cm. 求截面⊙O的半径.
求截面⊙O的半径.求截面中的劣弧AB的长.
