[江西]2012年江西省中等学校招生统一考试数学卷(一)
2010年江西省发生了特大洪灾,洪灾无情人有情,在此期间,社会各界高度关注灾情,纷纷慷慨相助,奉献爱心.从6月18日至6月29日16时,江西省民政厅救灾捐赠接收办公室共接收捐款3002.317万元,其中3002.317万这个数字(保留四个有效数字)用科学记数法表示为( )
A.3.002×10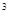 |
B.30.02×10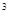 |
C.3.00231×10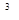 |
D.3.002×10 |
对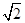 描述错误的一项是( )
描述错误的一项是( )
| A.面积为2的正方形的边长 | B.它是一个无限不循环小数 |
| C.它是2的一个平方根 | D.它的小数部分大于2-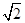 |
等腰三角形ABC在直角坐标系中,底边的两端点坐标是(-3,0),(5,0),则其顶点的坐标中能确定是( )
| A.横坐标 | B.纵坐标 |
| C.横坐标及纵坐标 | D.横坐标或纵坐标 |
在△ABC中,∠C=90°,若将各边长度都扩大为原来的3倍,则∠A的正弦值( )
| A.不变 | B.缩小3倍 | C.扩大3倍 | D.扩大9倍 |
下列说法不正确的是( )
A.方程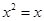 有一根为0 有一根为0 |
B.方程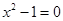 的两根互为相反数 的两根互为相反数 |
C.方程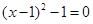 的两根互为相反数 的两根互为相反数 |
D.方程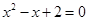 无实数根 无实数根 |
如图,河岸AD、BC互相平行,桥AB垂直于两岸,从C处看桥的两端A、B,夹角∠BCA=50 ,测得BC=10m,则桥长AB= m(用计算器计算,结果精确到0.1米)
,测得BC=10m,则桥长AB= m(用计算器计算,结果精确到0.1米)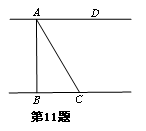
某县城2009年底商品房均价为2000元/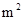 ,经过2010年第1季度和第2季度的涨价,商品房均价达3600元/
,经过2010年第1季度和第2季度的涨价,商品房均价达3600元/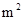 ,设每季度平均增长率为x,则可列方程为: .
,设每季度平均增长率为x,则可列方程为: .
以图1(以O为圆心,半径1 的半圆)作为“基本图形”,分别经历如下变换能得到图2的序号是 (多填或错填得0分,少填酌情给分)
①只要向右平移1个 单位;
② 先以直线AB为对称轴进行对称变换,再向右平移1个单位;
③先绕着O旋转180°,再向右平移1个单位;
④只要绕着某点旋转180°.
已知下列关于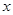 的分式方程:
的分式方程:
方程1. 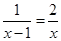 , 方程2.
, 方程2.  , 方程3.
, 方程3. 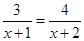 , ……,方程n,
, ……,方程n,填空:分式方程1的解为 ,分式方程2的解为 ;
解分式方程3;
根据上述方程的规律及解的特点,直接写出方程n及它的解.
如图1,是某单位的透空护栏,如图2是它的示意图,它是用外径为3cm的圆钢管与外圆直径为15cm的圆圈焊接而成的(圆圈由扁钢筋做成,两圆钢管之间夹一个圆圈),若要做高度统一为2m,长为7.41m的护栏.试问:需要圆钢管和展直扁钢筋的总长度各是多少m?
在2012年元旦期间有甲、乙两个小型超市举行有奖促销活动,顾客每购货20元就有一回按下面规则转盘获奖机会,且两超市奖额等同.规则是甲、乙两超市各把一转盘分成4个、3个区域,并标上了数字(如图甲、乙),顾客一回转盘要转两次,第一次与第二次分别停止后指针所指数字之和为奇数时就获奖(若指针停在等分线上,那么重转一次,直到指针指向某一份为止).利用树形图或列表法分别求出甲、乙两超市顾客一回转盘获奖的概率;
如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由.
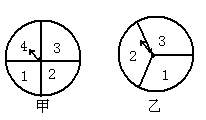
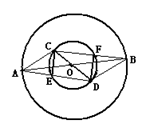
如图,同心⊙O,大⊙O的直径AB=2 ,小⊙O的直径CD=2,连接AC、AD、BD、BC,AD、CB分别交小⊙O于E、F.
,小⊙O的直径CD=2,连接AC、AD、BD、BC,AD、CB分别交小⊙O于E、F.问四边形CEDF是何种特殊四边形?请证明你的结论;
当AC与小⊙O相切时,四边形CEDF是正方形吗?请说明理由.
某校为了解初中生的交通安全知识掌握情况,在本校初中部随机抽取10﹪的学生,进行了交通安全知识测试,得分情况如下两个统计图,并约定85分及以上为优秀;73分~84分为良好;60分~72分为合格;59分及以下为不合格(满分为100分).在抽取的学生中,不合格人数所占的百分比是 ;
若不合格学生的总分恰好等于其他等级的某一个学生的分数,请推测这个学生是什么等级?并估算出该校初中部学生中共有多少人不合格?
试求所抽取的学生的平均分.
 .
.
已知抛物线m: ,顶点为A,若将抛物线m绕着点(1,0)旋转180°后得到抛物线n,顶点为C.
,顶点为A,若将抛物线m绕着点(1,0)旋转180°后得到抛物线n,顶点为C.当a=1时.试求抛物线n的顶点C的坐标,再求它的解析式;
在(1)中,请你分别在抛物线m、n上各取一点D、B(除点A、C外),
使得四边形ABCD为平行四边形(直接写出所取点的坐标,并至少写出二种情况);设抛物线m的对称轴与抛物线n的交点为P,且
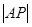 =6,试求a的值.
=6,试求a的值.
某班甲、乙、丙三位同学进行了一次用正方形纸片折叠探究相关数学问题的课题学习活动.
活动情境:
如图2,将边长为8cm的正方形纸片ABCD沿EG折叠(折痕EG分别与AB、DC交于点E、G),使点B落在AD边上的点 F处,FN与DC交于点M处,连接BF与EG交于点P.
所得结论:
当点F与AD的中点重合时:(如图1)甲、乙、丙三位同学各得到如下一个正确结论(或结果):
甲:△AEF的边AE= cm,EF= cm;
乙:△FDM的周长为16 cm;
丙:EG=BF.
你的任务:填充甲同学所得结果中的数据;
写出在乙同学所得结果的求解过程;
当点F在AD边上除点A、D外的任何一处(如图2)时:
① 试问乙同学的结果是否发生变化?请证明你的结论;
② 丙同学的结论还成立吗?若不成立,请说明理由,若你认为成立,先证明EG=BF,再求出S(S为四边形AEGD的面积)与x(AF=x)的函数关系式,并问当x为何值时,S最大?最大值是多少?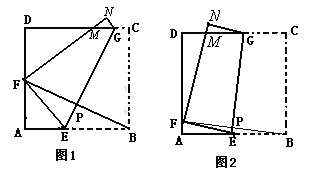


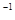
 +a
+a =a
=a

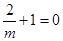
 的图象交
的图象交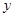 轴于负半轴,且
轴于负半轴,且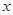 的增大而增大,请写出符合上述条件的一个解析式: .
的增大而增大,请写出符合上述条件的一个解析式: . 与
与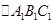 关于直线m对称,
关于直线m对称,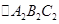 关于直线n对称,且有m//n,则
关于直线n对称,且有m//n,则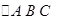 可以通过一次 变换直接得到
可以通过一次 变换直接得到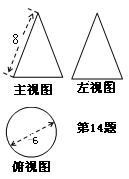
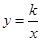 上,CD与y轴重合,则k的值是 .
上,CD与y轴重合,则k的值是 .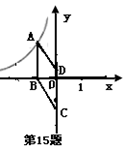
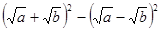 ,其中a=3,b=6.
,其中a=3,b=6.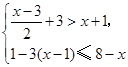 并在数轴上把解集表示出来.
并在数轴上把解集表示出来.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号