某校为了解初中生的交通安全知识掌握情况,在本校初中部随机抽取10﹪的学生,进行了交通安全知识测试,得分情况如下两个统计图,并约定85分及以上为优秀;73分~84分为良好;60分~72分为合格;59分及以下为不合格(满分为100分).在抽取的学生中,不合格人数所占的百分比是 ;
若不合格学生的总分恰好等于其他等级的某一个学生的分数,请推测这个学生是什么等级?并估算出该校初中部学生中共有多少人不合格?
试求所抽取的学生的平均分.
 .
.
相关知识点
推荐套卷
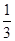 ,b=﹣
,b=﹣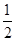 .
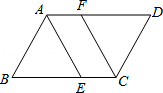
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号