如图一,AB是 的直径,AC是弦,直线EF和
的直径,AC是弦,直线EF和 相切与点C,
相切与点C, ,垂足为D.
,垂足为D.求证
 ;
;
如图二,若把直线EF向上移动,使得EF与
 相交于G,C两点(点C在点G的右侧),连结AC,AG,若题中其他条件不变,这时图中是否存在与
相交于G,C两点(点C在点G的右侧),连结AC,AG,若题中其他条件不变,这时图中是否存在与 相等的角?若存在,找出一个这样的角,并证明;若不存在,说明理由.
相等的角?若存在,找出一个这样的角,并证明;若不存在,说明理由.
如图, 为正方形
为正方形 对角线AC上一点,以
对角线AC上一点,以 为圆心,
为圆心, 长为半径的⊙
长为半径的⊙ 与
与 相切于点
相切于点 .
.
求证:
 与⊙
与⊙ 相切;
相切;若⊙
 的半径为1,求正方形
的半径为1,求正方形 的边长.
的边长.
已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分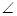 CAM交⊙O于D,过D作DE⊥MN于E.
CAM交⊙O于D,过D作DE⊥MN于E.求证:DE是⊙O的切线;
若
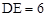 cm,
cm,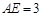 cm,求⊙O的半径.
cm,求⊙O的半径.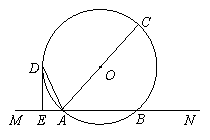
如图,有一块半圆形钢板,直径AB=20cm,计划将此钢板切割成下底为AB的等腰梯形,上底CD的端点在圆周上,且CD=10cm.求图中阴影部分的面积.
如图,已知⊙ 是以数轴的原点
是以数轴的原点 为圆心,半径为1的圆,
为圆心,半径为1的圆, ,点
,点 在数轴上运动,若过点
在数轴上运动,若过点 且与
且与 平行的直线与⊙
平行的直线与⊙ 有公共点, 设
有公共点, 设 ,则
,则 的取值范围是( )
的取值范围是( )
A.-1≤ ≤1 ≤1 |
B. ≤ ≤ ≤ ≤ |
C.0≤ ≤ ≤ |
D. > > |

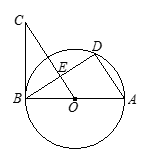
已知:如图,AB为⊙O的直径,AD为弦,∠DBC =∠A.
求证:BC是⊙O的切线;
若OC∥AD,OC交BD于E,BD=6,CE=4,求AD的长.
如图,在△AOB中,∠AOB= ,OA=OB=
,OA=OB= ,以点O为圆心的圆与AB相切于点C,则图中阴影部分的面积是______________.
,以点O为圆心的圆与AB相切于点C,则图中阴影部分的面积是______________.