[江西]2012届江西省中等学校招生统一考试数学卷(三)
如图,已知直线m∥n,直角三角板ABC的顶点A在直线m上,则∠α等于( )
| A.21° | B.48° | C.58° | D.30° |

在直角坐标系中,将双曲线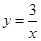 绕着坐标原点旋转90°后,所得到的双曲线的解析式是( )
绕着坐标原点旋转90°后,所得到的双曲线的解析式是( )
A.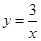 |
B.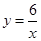 |
C.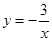 |
D.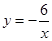 |
如图,一个圆形转盘被等分成五个扇形区域,上面分别标有数字1、2、3、4、5,转盘指针的位置固定,转动转盘后任其自由停止.转动转盘一次,当转盘停止转动时,记指针指向标有奇数所在区域的概率为 (奇数),则
(奇数),则 (奇数)等于( )
(奇数)等于( )
A. |
B. |
C. |
D. |

对于抛物线 ,下列说法错误的是( )
,下列说法错误的是( )
A.若顶点在x轴下方,则一元二次方程 有两个不相等的实数根 有两个不相等的实数根 |
B.若抛物线经过原点,则一元二次方程 必有一根为0 必有一根为0 |
C.若 ,则抛物线的对称轴必在y轴的左侧 ,则抛物线的对称轴必在y轴的左侧 |
D.若 ,则一元二次方程 ,则一元二次方程 ,必有一根为-2 ,必有一根为-2 |
如图,在平面直角坐标系中,点B(1,1),半径为1、圆心角为90°的扇形外周有一动点P,沿A→B→C→A运动一圈,则点P的纵坐标y随点P走过的路程s之间的函数关系用图象表示大致是( )
长度单位1纳米 米,目前发现一种新型病毒直径为23150纳米,用科学记数法表示该病毒直径是 米(保留两个有效数字)
米,目前发现一种新型病毒直径为23150纳米,用科学记数法表示该病毒直径是 米(保留两个有效数字)
如图,已知⊙O的半径为2cm,点C是直径AB的延长线上一点,且 ,过点C作⊙O的切线,切点为D,则CD= ★ cm.
,过点C作⊙O的切线,切点为D,则CD= ★ cm.
从10名学生(6男4女,其中小芳为女生)中,抽选6人参加“防震知识”竞赛.若规定男生选3人,则“选到小芳”的事件应该是 ★ (选填“必然事件、不可能事件、随机事件”).
刘谦的魔术表演风靡全国,小明也学起了刘谦、发明了一个魔术盒,当任意实数对 进入其中时,会得到一个新的实数
进入其中时,会得到一个新的实数 ,例如:把
,例如:把 放入其中,就会得到
放入其中,就会得到 . 现将实数对
. 现将实数对
 放入其中,得到实数24,则
放入其中,得到实数24,则 = ★ .
= ★ .
如图所示,一张矩形纸片沿BC折叠,顶点A落在点A′处,再过点A′折叠使折痕DE∥BC,若AB=4,AC=3,则△ADE的面积是 ★ .
如图,已知正方形边长为4,以A为圆心,AB为半径作 ,M是BC的中点,过点M作EM⊥BC交
,M是BC的中点,过点M作EM⊥BC交 于点E,则
于点E,则 的长为 ★ .
的长为 ★ .
如图,⊙O的半径OA⊥弦BC,且∠AOB=60°,D是⊙O上另一点,AD与BC相交于点E,若DC=DE,则正确结论的序号是 (多填或错填得0分,少填酌情给分).
① ; ②
; ② ; ③
; ③ ; ④△AEC∽△ACD.
; ④△AEC∽△ACD.
如图,点A, D, B,E在同一条直线上,且AD=BE, ∠A=∠FDE,则△ABC≌△DEF.判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题请给出一个适当的条件使它成为真命题,并加以证明.
如图,在平面直角坐标系中,A(2,1),B(5,2),C(3,4)是菱形ABDC的三个顶点.在图中画出菱形ABDC并写出菱形的顶点D的坐标,并求
 的值;
的值;以原点O为位似中心,将菱形ABDC放大为原来的2倍,在第一象限内画出放大后的图形,并写出点D的对应点D′的坐标.

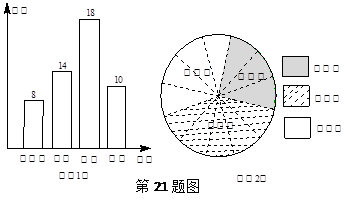
宣传交通安全知识,争做安全小卫士.某校进行“交通安全知识”宣传培训后进行了一次测试.学生考分按标准划分为不合格、合格、良好、优秀四个等级,为了解全校的考试情况,对在校的学生随机抽样调查,得到图(1)的条形统计图,请结合统计图回答下列问题:该校抽样调查的学生人数为_______名;抽样中考生分数的中位数所在等级是________;
抽样中不及格的人数是多少?占被调查人数的百分比是多少?
若已知该校九年级有学生500名,图(2)是各年级人数占全校人数百分比的扇形图(图中圆心角被等分),请你估计全校优良(良好与优秀)的人数约有多少人?
如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE.求证:AC=AE;
求△ACD外接圆的直径.

书籍是人类进步的阶梯!为爱护书一般都将书本用封皮包好.

现有精装词典长、宽、厚尺寸如图(1)所示(单位:cm),若按图(2)的包书方式,将封面和封底各折进去3cm.试用含a、b、c的代数式分别表示词典封皮(包书纸)的长是 cm,宽是___________cm;
在如图(4)的矩形包书纸皮示意图中,虚线为折痕,阴影是裁剪掉的部分,四角均为大小相同的正方形,正方形的边长即为折叠进去的宽度.
(1)若有一数学课本长为26cm、宽为18.5cm、厚为1cm,小海宝用一张面积为1260 cm2的矩形纸包好了这本数学书,封皮展开后如图(4)所示.若设正方形的边长(即折叠的宽度)为x cm,则包书纸长为 cm,宽为 cm(用含x的代数式表示).
(2)请帮小海宝列好方程,求出第(1)题中小正方形的边长x cm.
矩形OABC的顶点A(-8,0)、C(0,6) ,点D是BC边上的中点,抛物线 经过A、D两点,如图所示.
经过A、D两点,如图所示.求点D关于y轴的对称点
 的坐标及a、b的值;
的坐标及a、b的值;在y轴上取一点P, 使PA+PD长度最短, 求点P的坐标;
将抛物线
 向下平移,记平移后点A的对应点为
向下平移,记平移后点A的对应点为 ,点D的对应点为
,点D的对应点为 ,当抛物线平移到某个位置时,恰好使得点O是y轴上到
,当抛物线平移到某个位置时,恰好使得点O是y轴上到 两点距离之和
两点距离之和 最短的一点,求此抛物线的解析式.
最短的一点,求此抛物线的解析式.
在Rt△ABC中,∠ACB=90°,AB=4,D为AB的中点,将一直角△DEF纸片平放在△ACB所在的平面上,且使直角顶点重合于点D(C始终在△DEF内部),设纸片的两直角边分别与AC、BC相交于M、N.当∠A=∠NDB=45°时,四边形MDNC的面积为 ;
当∠A=45°,∠NDB≠45°时,四边形MDNC的面积是否与(1)相同?说明理由;
当∠A=∠NDB=30°时,四边形MDNC的面积为 ;
当∠A=30°,∠NDB≠30°时,四边形MDNC的面积是否发生变化?若不发生变化(即与(3)相同),说明理由,若发生变化,设四边形MDNC的面积为S,BN为
 ,求S与
,求S与 之间的关系.
之间的关系.
 ,则“
,则“ ”表示的数应是( )
”表示的数应是( )






 的自变量x的取值范围是( ★ )
的自变量x的取值范围是( ★ )



 ___★___.
___★___.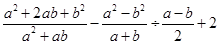 ,其中
,其中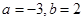 .
.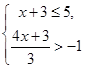 ,并求它的整数解.
,并求它的整数解. 粤公网安备 44130202000953号
粤公网安备 44130202000953号