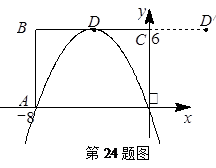矩形OABC的顶点A(-8,0)、C(0,6) ,点D是BC边上的中点,抛物线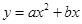 经过A、D两点,如图所示.
经过A、D两点,如图所示.求点D关于y轴的对称点
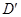 的坐标及a、b的值;
的坐标及a、b的值;在y轴上取一点P, 使PA+PD长度最短, 求点P的坐标;
将抛物线
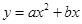 向下平移,记平移后点A的对应点为
向下平移,记平移后点A的对应点为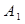 ,点D的对应点为
,点D的对应点为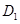 ,当抛物线平移到某个位置时,恰好使得点O是y轴上到
,当抛物线平移到某个位置时,恰好使得点O是y轴上到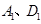 两点距离之和
两点距离之和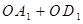 最短的一点,求此抛物线的解析式.
最短的一点,求此抛物线的解析式.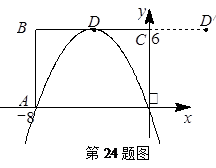
相关知识点
推荐套卷
矩形OABC的顶点A(-8,0)、C(0,6) ,点D是BC边上的中点,抛物线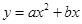 经过A、D两点,如图所示.
经过A、D两点,如图所示.求点D关于y轴的对称点
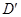 的坐标及a、b的值;
的坐标及a、b的值;在y轴上取一点P, 使PA+PD长度最短, 求点P的坐标;
将抛物线
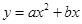 向下平移,记平移后点A的对应点为
向下平移,记平移后点A的对应点为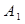 ,点D的对应点为
,点D的对应点为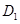 ,当抛物线平移到某个位置时,恰好使得点O是y轴上到
,当抛物线平移到某个位置时,恰好使得点O是y轴上到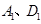 两点距离之和
两点距离之和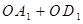 最短的一点,求此抛物线的解析式.
最短的一点,求此抛物线的解析式.