如图,在平面直角坐标系中,一次函数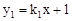 的图象与y轴交于点A,
的图象与y轴交于点A,
与x轴交于点B,与反比例函数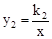 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
标为2,
(1)求一次函数和反比例函数的解析式;
(2)直接写出 时x的取值范围。
时x的取值范围。
相关知识点
推荐套卷
如图,在平面直角坐标系中,一次函数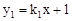 的图象与y轴交于点A,
的图象与y轴交于点A,
与x轴交于点B,与反比例函数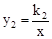 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
标为2,
(1)求一次函数和反比例函数的解析式;
(2)直接写出 时x的取值范围。
时x的取值范围。