初中数学三角形的五心试题

（本题12分）如图，ABCD是一张矩形纸片，AD=BC=1,AB=CD=5．在矩形ABCD的边AB上取一点M，在CD上取一点N，将纸片沿MN折叠，使MB与DN交于点K，得到△MNK．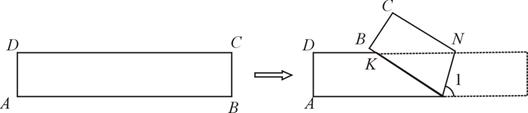

（1）若∠1=70°，求∠MKN的度数．
（2）△MNK的面积能否小于？若能，求出此时∠1的度数；若不能，试说明理由．
（3）如何折叠能够使△MNK的面积最大？请你利用备用图探究可能出现的情况，求出最大值．

已知△ABC，以AC为边在△ABC外作等腰△ACD，其中AC=AD．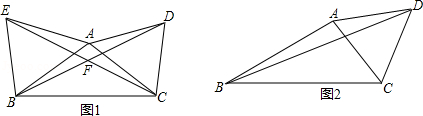

（1）如图1，若AB=AE，∠DAC=∠EAB=60°，求∠BFC的度数；
（2）如图2，∠ABC=α，∠ACD=β，BC=4，BD=6．
①若α=30°，β=60°，AB的长为；
②若改变α，β的大小，但α+β=90°，△ABC的面积是否变化？若不变，求出其值；若变化，说明变化的规律．

如图，矩形ABCD中，AB=8，BC=6，P为AD上一点，将△ABP沿BP翻折至△EBP，PE与CD相交于点O，且OE=OD，则AP的长为__________．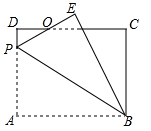

如图1，将两块全等的直角三角形纸片△ABC和△DEF叠放在一起，其中∠ACB=∠E=90°，BC=DE=6，AC=FE=8，顶点D与边AB的中点重合．
（1）若DE经过点C，DF交AC于点G，求重叠部分（△DCG）的面积；
（2）合作交流：“希望”小组受问题（1）的启发，将△DEF绕点D旋转，使DE⊥AB交AC于点H，DF交AC于点G，如图2，求重叠部分（△DGH）的面积．

如图，在直角坐标系中，已知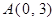、、、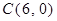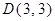，点P从C点出发，沿着折线C﹣D﹣A运动到达点A时停止，过C点作直线GC⊥PC，且与过O、P、C三点的⊙M交于点G，连接OP、PG、OD．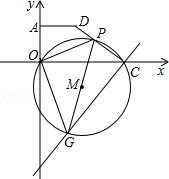

（1）直接写出∠DCO的度数；
（2）当点P在线段CD上运动时，求△OPG的最小面积；
（3）设圆心M的纵坐标为n，试探索：在点P运动的整个过程中，n的取值范围．

如图，在梯形ABCD中，AD∥BC，BE平分∠ABC交CD于E，且BE⊥CD，CE:ED=2:1．如果△BEC的面积为2，那么四边形ABED的面积是 ．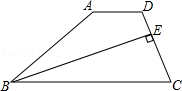

如图，在△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠BAC=50°，∠C=70°．求∠DAC和∠BOA的度数．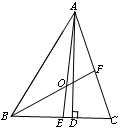

如图，在△ABC中，BA=BC，D在边CB上，且DB=DA=AC．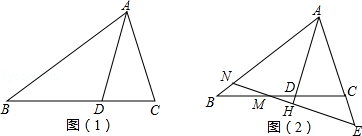

（1）如图1，填空∠B= °，∠C= °；
（2）若M为线段BC上的点，过M作直线MH⊥AD于H，分别交直线AB、AC与点N、E，如图2
①求证：△ANE是等腰三角形；
②试写出线段BN、CE、CD之间的数量关系，并加以证明．

如图，AD⊥BC，垂足为D．CD=1，AD=2，BD=4．

（1）求∠BAC的度数？并说明理由；
（2）P是边BC上一点，连结AP，当△ACP为等腰三角形时，求CP的长．

如图，在△ABC中，∠ACB＝90°，AC＝BC，AE为BC边上的中线，CD⊥AE于点F，BD⊥BC于点B．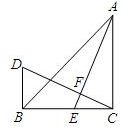

（1）试说明：AE＝CD；
（2）若AC＝10cm，求线段BD的长．

如图，已知∠MON＝30°，点A₁、A₂、A₃…在射线ON上，点B₁、B₂、B₃…在射线OM上；
△A₁B₁A₂、△A₂B₂A₃、△A₃B₃A₄…均为等边三角形．若OA₁＝1，则△A₂₀₁₅B₂₀₁₅A₂₀₁₆的边长为…（）

A．4028

B．4030

C．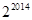

D．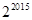

如图1，已知锐角△ABC中，CD．BE分别是AB、AC边上的高，M、N分别是线段BC、DE的中点．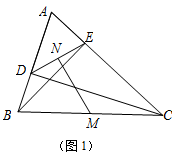

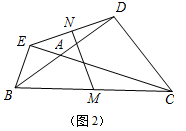
（1）连接DM，ME，猜想∠A与∠DME之间的关系，并写出推理过程；
（2）求证：MN⊥DE；
（3）若将锐角△ABC变为钝角△ABC，如图2，上述（1）（2）中的结论是否都成立，若结论成立，直接回答，不需证明；若结论不成立，请说明理由．

问题提出：用n根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？
问题探究：不妨假设能搭成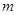种不同的等腰三角形，为探究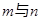之间的关系，我们可以从特殊入手，通过试验、观察、类比，最后归纳、猜测得出结论．
探究一：
用3根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
此时，显然能搭成一种等腰三角形。所以，当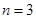时，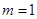
用4根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
只可分成1根木棒、1根木棒和2根木棒这一种情况，不能搭成三角形
所以，当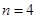时，
用5根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
若分成1根木棒、1根木棒和3根木棒，则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒，则能搭成一种等腰三角形
所以，当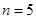时，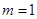
用6根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
若分成1根木棒、1根木棒和4根木棒，则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒，则能搭成一种等腰三角形
所以，当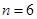时，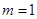
综上所述，可得表①

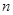	3	4	5	6
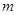	1	0	1	1

探究二：
用7根相同的木棒搭成一个三角形，能搭成多少种不同的等腰三角形？
（仿照上述探究方法，写出解答过程，并把结果填在表②中）
分别用8根、9根、10根相同的木棒搭成一个三角形，能搭成多少种不同的等腰三角形？（只需把结果填在表②中）

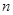	7	8	9	10

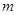你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究，……
解决问题：用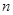根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？
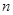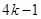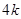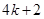（设分别等于、、、，其中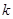是整数，把结果填在表③中）

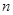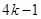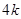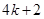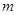问题应用：用2016根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？（要求写出解答过程）
其中面积最大的等腰三角形每个腰用了__________________根木棒。（只填结果）

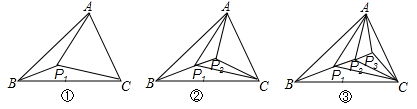
如图，△ABC的三个顶点和它内部的点P₁，把△ABC分成3个互不重叠的小三角形；△ABC的三个顶点和它内部的点P₁、P₂，把△ABC分成5个互不重叠的小三角形；△ABC的三个顶点和它内部的点P₁、P₂、P₃，把△ABC分成7个互不重叠的小三角形；……，△ABC的三个顶点和它内部的点P₁、P₂、P₃……Pn，把△ABC分成 个互不重叠的小三角形．

11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”的问题：小溪边长着两棵棕榈树，恰好隔岸相望．一棵树高是30肘尺（肘尺是古代的长度单位），另外一棵高20肘尺；两棵棕榈树的树干间的距离是50肘尺．每棵树的树顶上都停着一只鸟．忽然，两只鸟同时看见棕榈树间的水面上游出一条鱼，它们立刻以相同的速度飞去抓鱼，并且同时到达目标．问这条鱼出现的地方离开比较高的棕榈树的树跟有多远？