初中数学三角形的五心试题

（本小题满分8分）如图，平面直角坐标系中，将含30°的三角尺的直角顶点C落在第二象限．其斜边两端点A、B分别落在x轴、y轴上，且AB=12cm

（1）若OB=6cm．
①求点C的坐标；
②若点A向右滑动的距离与点B向上滑动的距离相等，求滑动的距离；
（2）点C与点O的距离的最大值．

如图，△A₁A₂B是直角三角形，∠A₁A₂B=90⁰，且A₁A₂＝A₂B＝4， A₂A₃⊥A₁B，垂足为A₃，A₃A₄⊥A₂B，垂足为A₄，A₄A₅⊥A₃B，垂足为A₅，A₅A₆⊥A₄B，垂足为A₆，一直按此做去，……则△A_nA_n+1B的面积为 ．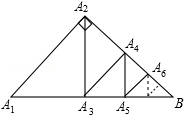

（1）如图1，已知△ABC，以AB、AC为边向△ABC外作等边△ABD和等边△ACE，连接BE，CD，请你完成图形（尺规作图，保留作图痕迹），并猜想BE与CD的关系：___________；你是通过证明_______________ 得到的；
（2）如图2，已知△ABC，以AB、AC为边向外作正方形ABFD和正方形ACGE，连接BE，CD，BE与CD有什么数量关系？并说明理由；
（3）运用（1）、（2）解答中所积累的经验和知识，完成下题：
如图3，要测量池塘两岸相对的两点B，E的距离，已经测得∠ABC=45°，∠CAE=90°，AB=BC=100米，AC=AE，求BE的长．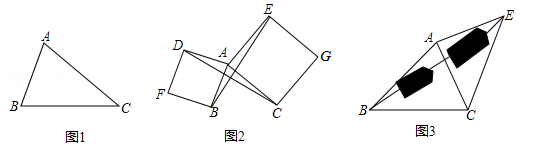

如图，七星形中∠A+∠B+∠C+∠D+∠E+∠F+∠G＝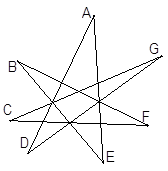

小明遇到这样一个问题：已知：在△ABC中，AB，BC，AC三边的长分别为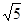、、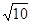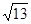，求△ABC的面积．
小明是这样解决问题的：如图1所示，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），从而借助网格就能计算出△ABC的面积．他把这种解决问题的方法称为构图法．请回答：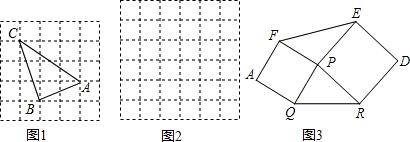

（1）求图1中△ABC的面积；
参考小明解决问题的方法，完成下列问题：
（2）图2是一个6×6的正方形网格（每个小正方形的边长为1）．
①利用构图法在答题卡的图2中画出三边长分别为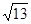、、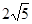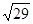的格点△DEF；
②计算△DEF的面积是 ．
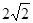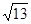（3）如图3，已知△PQR，以PQ，PR为边向外作正方形PQAF，PRDE，连接EF．若PQ=，PR=，QR=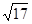，求六边形AQRDEF的面积．

如图，矩形ABCD中，AB=8，BC=6，P为AD上一点，将△ABP沿BP翻折至△EBP，PE与CD相交于点O，且OE=OD，则AP的长为__________．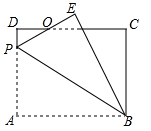

如图1，将两块全等的直角三角形纸片△ABC和△DEF叠放在一起，其中∠ACB=∠E=90°，BC=DE=6，AC=FE=8，顶点D与边AB的中点重合．
（1）若DE经过点C，DF交AC于点G，求重叠部分（△DCG）的面积；
（2）合作交流：“希望”小组受问题（1）的启发，将△DEF绕点D旋转，使DE⊥AB交AC于点H，DF交AC于点G，如图2，求重叠部分（△DGH）的面积．

如图，在△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠BAC=50°，∠C=70°．求∠DAC和∠BOA的度数．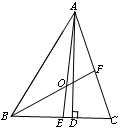

如图，已知∠MON＝30°，点A₁、A₂、A₃…在射线ON上，点B₁、B₂、B₃…在射线OM上；
△A₁B₁A₂、△A₂B₂A₃、△A₃B₃A₄…均为等边三角形．若OA₁＝1，则△A₂₀₁₅B₂₀₁₅A₂₀₁₆的边长为…（）

A．4028

B．4030

C．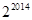

D．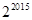

如图△ABC中，AB=10，AC=6，中线AD=4，则BC长是 ．

如图，△ABC的三个顶点和它内部的点P₁，把△ABC分成3个互不重叠的小三角形；△ABC的三个顶点和它内部的点P₁、P₂，把△ABC分成5个互不重叠的小三角形；△ABC的三个顶点和它内部的点P₁、P₂、P₃，把△ABC分成7个互不重叠的小三角形；……，△ABC的三个顶点和它内部的点P₁、P₂、P₃……Pn，把△ABC分成 个互不重叠的小三角形．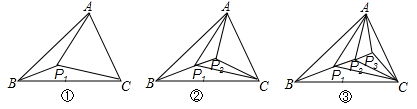

11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”的问题：小溪边长着两棵棕榈树，恰好隔岸相望．一棵树高是30肘尺（肘尺是古代的长度单位），另外一棵高20肘尺；两棵棕榈树的树干间的距离是50肘尺．每棵树的树顶上都停着一只鸟．忽然，两只鸟同时看见棕榈树间的水面上游出一条鱼，它们立刻以相同的速度飞去抓鱼，并且同时到达目标．问这条鱼出现的地方离开比较高的棕榈树的树跟有多远？

如图，在△ABC中，∠ACB＝90°，AC＝BC，AE为BC边上的中线，CD⊥AE于点F，BD⊥BC于点B．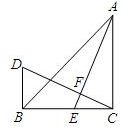

（1）试说明：AE＝CD；
（2）若AC＝10cm，求线段BD的长．

如图所示，已知AC∥BD，EA，EB分别平分∠CAB和∠DBA，CD过E点．求证：AB＝AC＋BD．

问题提出：用n根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？
问题探究：不妨假设能搭成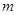种不同的等腰三角形，为探究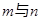之间的关系，我们可以从特殊入手，通过试验、观察、类比，最后归纳、猜测得出结论．
探究一：
用3根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
此时，显然能搭成一种等腰三角形。所以，当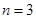时，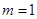
用4根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
只可分成1根木棒、1根木棒和2根木棒这一种情况，不能搭成三角形
所以，当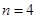时，
用5根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
若分成1根木棒、1根木棒和3根木棒，则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒，则能搭成一种等腰三角形
所以，当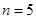时，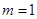
用6根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
若分成1根木棒、1根木棒和4根木棒，则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒，则能搭成一种等腰三角形
所以，当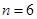时，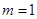
综上所述，可得表①

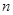	3	4	5	6
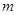	1	0	1	1

探究二：
用7根相同的木棒搭成一个三角形，能搭成多少种不同的等腰三角形？
（仿照上述探究方法，写出解答过程，并把结果填在表②中）
分别用8根、9根、10根相同的木棒搭成一个三角形，能搭成多少种不同的等腰三角形？（只需把结果填在表②中）

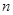	7	8	9	10

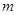你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究，……
解决问题：用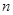根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？
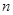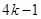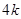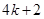（设分别等于、、、，其中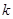是整数，把结果填在表③中）

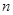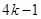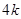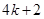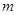问题应用：用2016根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？（要求写出解答过程）
其中面积最大的等腰三角形每个腰用了__________________根木棒。（只填结果）