如图,已知在Rt△ABC中,AB=35,一个边长为12的正方形CDEF内接于△ABC.则△ABC的周长为( ). 
(A)35(B)40(C)81(D)84
在等边三角形ABC所在的平面内存在点P,使⊿PAB、⊿PBC、⊿PAC都是等腰三角形.请指出具有这种性质的点P的个数()
(A)1(B)7(C)10(D)15
在Rt△ABC中,∠B=60°,∠C=90°,AB=1,分别以AB、BC、CA为边长向△ABC外作等边△ABR、等边△BCP、等边△CAQ,联结QR交AB于点T.则△PRT的面积等于( ).
(A)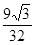 (B)
(B)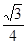 (C)
(C) (D)
(D)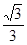
如图,D、E分别为△ABC的边AB、AC上的点,△ACD与△BCD的周长相等,△ABE与△CBE的周长相等,记△ABC的面积为S.若∠ACB=90°,则AD·CE与S的大小关系为( ). 
A、S=AD·CE B、S>AD·CE C、S<AD·CE D、无法确定
设a、b、c和S分别为三角形的三边长和面积,关于x的方程b2x2+(b2+c2-a2)x+c2=0的判别式为Δ.则Δ与S的大小关系为( ).
| A.Δ=16S2 | B.Δ=-16S2 | C.Δ=16S | D.Δ=-16S |
在下列图形中,各有一边长为4cm的正方形与一个8cm×2cm的长方形相重叠.问哪一个重叠的面积最大()
在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),连结AD,作∠ADE=∠B=α,DE交AC于点E,且cosα= .有下列结论:①△ADE∽△ACD; ②当BD=6时,△ABD与△DCE全等;③当△DCE为直角三角形时,BD=8;④3.6≤AE<10.其中正确的结论是()
.有下列结论:①△ADE∽△ACD; ②当BD=6时,△ABD与△DCE全等;③当△DCE为直角三角形时,BD=8;④3.6≤AE<10.其中正确的结论是()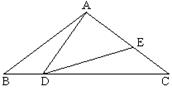
| A.①③ | B.①④ | C.①②④ | D.①②③ |
已知D、E、F分别为等腰△ABC边BC、CA、AB上的点,如果AB=AC,BD=2,CD=3,CE=4,AE=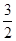 ,∠FDE=∠B,那么AF的长为()
,∠FDE=∠B,那么AF的长为()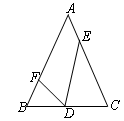
A.5.5B.4.5 C.4D.3.5
如图,在图1中, 、
、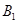 、
、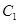 分别是等边△ABC的边BC、CA、AB的中点,在图2中,
分别是等边△ABC的边BC、CA、AB的中点,在图2中,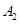 、
、 、
、 分别是△
分别是△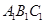 的边
的边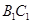 、
、 、
、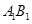 的中点,……,按此规律,则第n个图形中菱形的个数共有()个
的中点,……,按此规律,则第n个图形中菱形的个数共有()个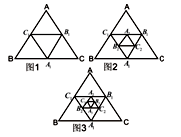
A.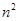 B.2n C.3n D.3n+1
B.2n C.3n D.3n+1
如图,四边形ABCD中,∠C= ,∠B=∠D=
,∠B=∠D=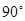 ,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF的度数为().
,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF的度数为().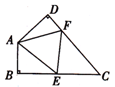
A. |
B.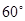 |
C. |
D.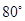 |
如果三角形满足一个角是另一个角的4倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能作为一个智慧三角形三边长的一组是()
| A.1,2,3 | B.1,1,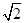 |
C.1,1,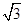 |
D.1,2,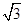 |
如图,△ABC与△DEF都是等腰三角形,且AB=AC=3,DE=DF=2,若∠B+∠E=90°,则△ABC与△DEF的面积比为()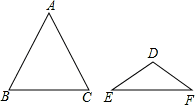
| A.9:4 | B.3:2 | C.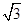 : : |
D.3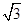 :2 :2 |
如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有()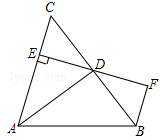
| A.4个 | B.3个 | C.2个 | D.1个 |
如图,已知∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上;
△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形.若OA1=1,则△A2015B2015A2016的边长为…()
| A.4028 | B.4030 | C.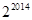 |
D.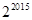 |